(ادامه) توزیع های احتمالی در نرم افزار مینی تب | تصویری
آموزش توزیع های احتمالی در مینی تب
آموزش توزیع های احتمالی در مینی تب، سلام و خسته نباشید خدمت همراهان صنایع سافت.دوستان قصد داریم در این قسمت از اموزش نرم افزارهای مهندسی صنایع، نرم افزار مینی تب که یک نرم افزار آماری برای مهندسان صنایع و هر کسی که به نحوی با آمار سروکار دارد، بپردازیم.
در این اموزش موارد زیر را بررسی خواهیم کرد:
- آشنایی با برخی از توابع توزیع
- مقدمه ای بر احتمالات و متغیر تصادفی
- توزیع های گسسته
- توزیع دو جمله ای
- محاسبه احتمال یک متغیر تصادفی با توزیع دو جمله ای با Minitab
- توزیع پوآسون
- محاسبه احتمال یک متغیر تصادفی با توزیع پوآسون با Minitab
- توزیع های پیوسته
- توزیع نرمال
- محاسبه احتمال توزیع نرمال با Minitab
- محاسبه احتمال توزیع مربع کای با Minitab
- محاسبه احتمال توزیع t با Minitab
- محاسبه احتمال توزیع F با Minitab
- پیدا کردن تابع توزیع یک متغیر تصادفی
- پیدا کردن تابع توزیع یک متغیر تصادفی با Minitab
مقدمه ای بر احتمالات و متغیر تصادفی
در دنیای واقعی به ندرت پیش می آید مواردی که بررسی می کنید قطعی باشد, معمولا همه چیز احتمالی می باشد برای مثال مدت زمان ورود افراد به یک بانک, ضخامت کاغذ های تولید شده در یک فرآیند تولید کاغذ, عمر لامپ های تولید شده در یک فرآیند تولید لامپ و… علم آمار به ما این کمک را می کند که با شناخت و تحلیل های مناسب بهترین تصمیم را بگیریم.
در واقع هر چیزی که یک متغیر باشد را به آن متغیر گوییم و هر متغیری که احتمالی باشد را یک متغیر تصادفی گوییم. این متغیرها می توانند پیوسته یا گسسته باشند. برای مثال تعداد افرادی که در یک مدت زمان معین وارد بانک می شوند, یک متغیر تصادفی گسسته می باشد اما مدت زمان بین ورود افراد به بانک یک متغیر تصادفی پیوسته می باشد.
هر متغیر تصادفی یک تابع توزیع احتمال دارد که به وسیله آن تابع توزیع می توان احتمال وقوع یک پیشامد را پیدا کرد. در ادامه به معرفی برخی از تابع توزیع هایی که بیشتر از آن ها استفاده می کنیم, می پردازیم. توجه داشته باشید که در کنترل کیفیت به متغیرهای تصادفی پیوسته, مشخصه کیفی متغیر و به متغیرهای تصادفی گسسته, مشخصه های کیفی وصفی می گویند.
توزیع های گسسته
در این تابع توزیع ها X یک متغیر تصادفی گسسته می باشد. مقادیر ممکن X می تواند محدود یا نامحدود باشد.
۱- توزیع دو جمله ای
در این توزیع متغیر تصادفی X پیشامد تعداد موفقیت ها در n آزمایش می باشد به طوریکه در هر آزمایش با احتمال P می بریم و با احتمال P-1 می بازیم. تابع توزیع X به صورت زیر می باشد :
![]()
میانگین واقعی و واریانس برای متغیر تصادفی X با توزیع دوجمله ای به صورت زیر می باشد:
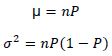
در نظر داشته باشید که هرگاه تعداد نمونه زیاد و احتمال موفقیت در هر نمونه پایین باشد (۵ > np) برای محاسبه احتمال یک متغیر تصادفی با توزیع دوجمله ای از تقریب های پوآسون و نرمال استفاده می کنند.
محاسبه احتمال یک متغیر تصادفی با توزیع دو جمله ای با Minitab
مثال: فرض کنید در یک فرآیند تولید احتمال اینکه یک قطعه معیوب باشد، ۲.۰ است. اگر یک نمونه ۲۲ تایی گرفته شود آنگاه مطلوبست:
- احتمال اینکه ۵ قطعه میعوب دیده شود؟
- احتمال اینکه حداکثر ۵ قطعه معیوب دیده شود؟
- حداکثر تعداد اقلام معیوب چه قدر باشد تا با احتمال حداقل ۲.۶ پی به وجود آن ببریم؟
برای حل قسمت الف ابتدا مسیر زیر را دنبال کنید:
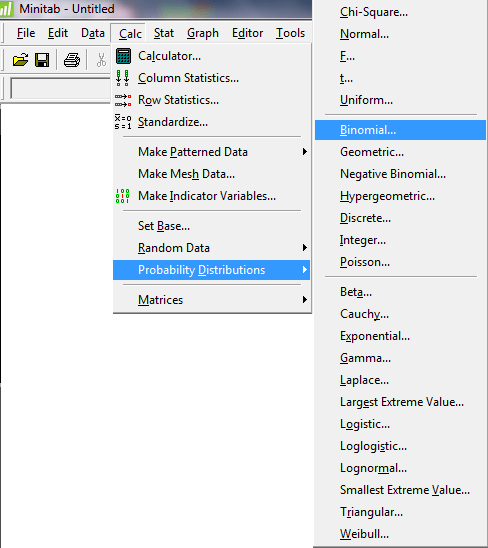
در پنجره Binomial distribution در صورتیکه می خواهید (P(X=x را محاسبه کنید گزینه Probability را انتخاب کنید و در صورتیکه می خواهید (p(X≤x را محاسبه کنید گزینه Cumulative probability را انتخاب کنید.
و اگر می خوهید احتمال تجمعی معکوس یا عدد a را در p(X≤a) =P محاسبه کنید گزینه Inverse cumulative probability را انتخاب کنید. این سه گزینه در محاسبه احتمال همه ی تابع توزیع های گسسته وجود دارد و توضیحاتی که داده شده برای همه ی آن ها صادق است.
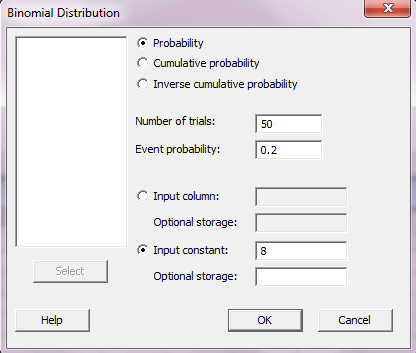
برای حل قسمت الف این سوال گزینه Probability را انتخاب کرده و در کادر مقابل Number of trial تعداد آزمایش ها را وارد کنید که در این مثال برابر ۵۰ می باشد و در قسمت Event probability احتمال موفقیت در هر آزمایش یا همان P را وارد کنید که در این مثال برابر ۰.۲ می باشد هم چنین در قسمت Input constant عدد ۸ را وارد کنید و OK را بزنید.
توجه داشته باشید که اگر می خواهید احتمال پیشامد های مختلفی را که در یک ستون وارد کردید محاسبه کنید ,گزینه ی Input column را انتخاب کنید و ستون مورد نظر را وارد کنید.
Probability Density Function
Binomial with n = 50 and p = 0.2
x P( X = x )
۸ ۰.۱۱۶۹۲۲
تحلیل: احتمال اینکه ۸ کالای معیوب در یک نمونه ی ۵۰ تایی ببنیم برابر ۰.۱۱ می باشد.
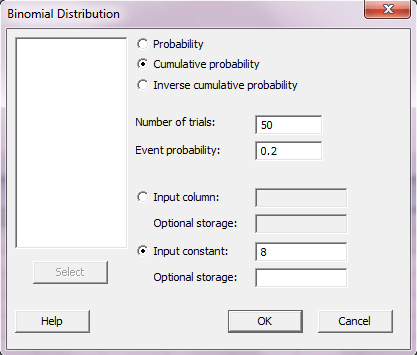
برای حل قسمت ب این سوال در پنجره Binomial distribution فقط کافیست به جای گزینه ی Probability , گزینه Cumulative probability را انتخاب کرده و OK را بزنید.
Cumulative Distribution Function
Binomial with n = 50 and p = 0.2
x P( X <= x )
۸ ۰.۳۰۷۳۳۲
تحلیل: احتمال اینکه حداکثر ۸ کالای معیوب در یک نمونه ی ۵۰ تایی ببینیم برابر ۰.۳ می باشد.
برای حل قسمت ج سوال اینبار در پنجره Binomial distribution گزینه ی Inverse cumulative distribution انتخاب کرده و در کادر مقابل Input constant عدد ۲.۶ را وارد کنید و OK را بزنید.
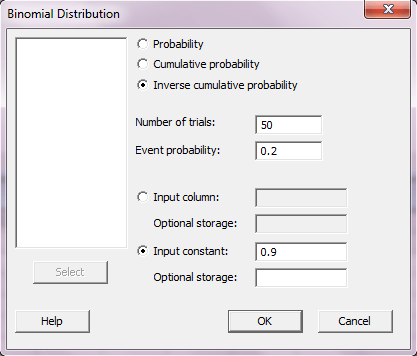
Inverse Cumulative Distribution Function
Binomial with n = 50 and p = 0.2
x P( X <= x ) x P( X <= x )
۱۳ ۰.۸۸۹۴۱۳ ۱۴ ۰.۹۳۹۲۷۸
تحلیل: همانطور که مشاهده می کنید احتمال دیده شدن حداکثر ۱۳ معیوب در ۵۰ نمونه ۰.۸۸ و احتمال دیده شدن حداکثر ۱۴ معیوب برابر ۰.۹۳ می باشد پس اگر ۱۴ معیوب در این ۵۰ نمونه وجود داشته باشد با احتمال ۰.۹۳ قابل کشف خواهد بود.
توزیع پوآسون
در این توزیع متغیر تصادفی X پیشامد تعداد رویدادها در یک بازه زمانی یا مکانی می باشد به طوریکه λ متوسط تعداد رویدادها در همان بازه زمانی یا مکانی می باشد.
در صورتیکه X متغیر تصادفی با توزیع پوآسون باشد, میانگین واقعی و واریانس این متغیر تصادفی هر دو برابر λ است.توزیع پوآسون تنها تابع توزیعی می باشد که میانگین و واریانس آن با هم برابر است.
محاسبه احتمال یک متغیر تصادفی با توزیع پوآسون با Minitab
مثال: فرض کنید متوسط تعداد غلط های تایپی در یک صفحه از یک کتاب ۲۰۰ صفحه ای, دو تا می باشد. آن گاه مطلوبست احتمال اینکه:
- احتمال اینکه تنها سه غلط در یک صفحه ی این کتاب دیده شود؟
- احتمال اینکه حداکثر سه غلط در یک صفحه این کتاب دیده شود؟
- حداکثر چند غلط تایپی در یک صفحه کتاب وجود داشته باشد تا با احتمال حداقل ۰.۹ پی به وجود آن ببریم؟
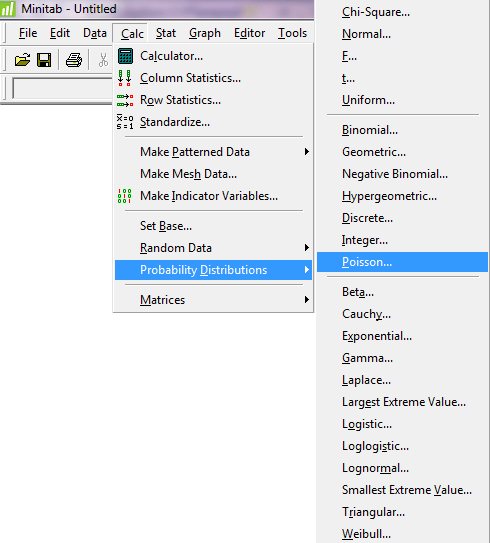
برای حل سه قسمت این سوال مسیر زیر را دنبال کنید:
در پنجره Poisson distribution گزینه Probability را انتخاب کنید و در کادر مقابل Mean مقدار λ را وارد کنید که برابر ۲ می باشد هم چنین با انتخاب گزینه Input constant و وارد کردن عدد ۳ می توانید قسمت ۱ این سوال را حل کنید.
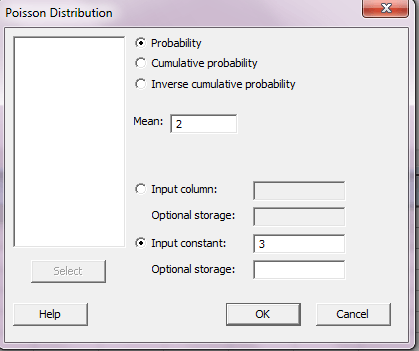
Probability Density Function
Poisson with mean = 2
x P( X = x )
۳ ۰.۱۸۰۴۴۷
تحلیل: همانطور که مشاهده می کنید احتمال اینکه در یک صفحه خاص سه غلط تایپی دیده شود برابر ۰.۱۸ می باشد.
برای حل قسمت ۲ این سوال فقط کافیست به جای گزینه ی Probability، گزینه ی Cumulative probability را بزنید و در پنجره Poisson distribution انتخاب کنید و OK را بزنید.
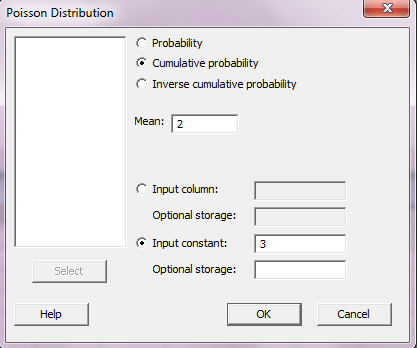
Cumulative Distribution Function
Poisson with mean = 2
x P( X <= x )
۳ ۰.۸۵۷۱۲۳
تحلیل: همانطور که از خروجی صفحه Session پیدا ست احتمال اینکه حداکثر سه غلط تایپی در یک صفحه ببینیم برابر ۰.۸۵ می باشد.
برای حل قسمت ۳ سوال در پنجره Poisson distribution گزینه Inverse cumulative probability را انتخاب کرده و در کادر مقابل Input constant عدد ۰.۹ را وارد کرده و OK را بزنید.
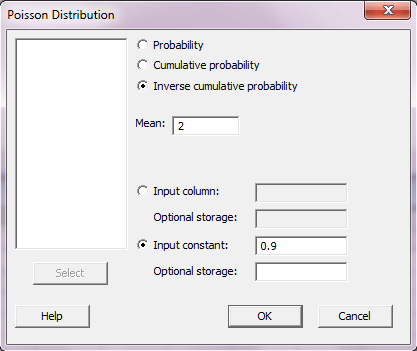
Inverse Cumulative Distribution Function
Poisson with mean = 2
x P( X <= x ) x P( X <= x )
۳ ۰.۸۵۷۱۲۳ ۴ ۰.۹۴۷۳۴۷
تحلیل : در صورتیکه حداکثر ۴ غلط تایپی در یک صفحه ی کتاب وجود داشته باشد شما با احتمال ۰.۹۴ پی به وجود این ۴ غلط خواهید برد.
توزیع های پیوسته
در این تابع توزیع ها , X پیشامد یک متغیر تصادفی پیوسته می باشد. مقادیر ممکن X می تواند بی کران یا کراندار باشد.
توزیع نرمال
توزیع نرمال حالت خاصی از توزیع گاما می باشد به طوریکه X پیشامد یک متغیر تصادفی پیوسته با میانگین µ و انحراف معیار σ می باشد.
از آنجاییکه برای محاسبه ی هر احتمالی باید از تابع توزیع فوق انتگرال گرفت، و هر انتگرالی از تابع فوق غیر قابل حل می باشد، پس از تغییر متغیر x-µ/σ=Z برای محاسبه ی هر احتمالی استفاده می شود که به Z مقدار استاندارد شده گویند و در صورتیکه X دارای توزیع نرمال با میانگین µ و انحراف معیار σ باشد، آن گاه Z دارای توزیع نرمال با میانگین صفر و انحراف معیار یک می باشد.
نمودار تابع چگالی احتمال نرمال به صورت زیر می باشد:
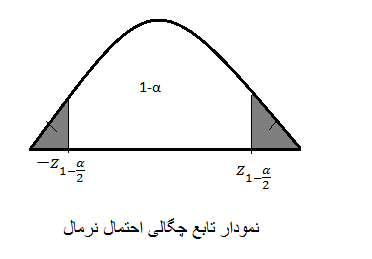
محاسبه احتمال توزیع نرمال با Minitab
مثال: فرض کنید ضخامت نورد های تولید شده در فرآیند تولید نورد دارای توزیع نرمال با میانگین ۲ و انحراف معیار ۰.۱ میلی متر می باشد. آن گاه مطلوبست احتمال اینکه:
- احتمال اینکه ضخامت نورد تولید شده حداکثر ۰.۰ میلی متر باشد؟
- ضخامت نورد تولید شده حداکثر چه قدر باشد تا با احتمال ۲.۶۴۲ قابل کشف باشد؟
- اگر یک نمونه ی ۶ تایی از این فرآیند گرفته شود, احتمال اینکه میانگین نمونه حداکثر برابر ۰.۰ میلی متر شود چه قدر است؟
برای حل دو قسمت این سوال مسیر زیر را دنبال کنید:
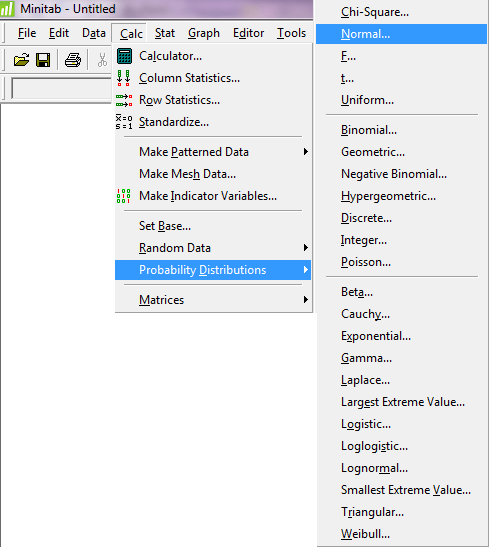
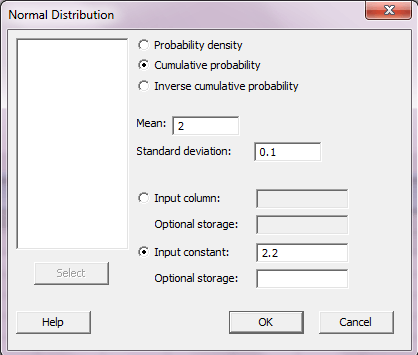
در صورتیکه می خواهید X≤x)P) را محاسبه کنید گزینه Cumulative probability را انتخاب کنید، اما اگر می خواهید مقدار معکوس یک احتمال تجمعی را به دست آورید, گزینه Inverse cumulative probability را انتخاب کنید. برای حل قسمت ۱ این سوال گزینه Cumulative probability را انتخاب کرده و در کادر مقابل Mean و Standard deviation مقدار میانگین و انحراف معیار را که هر یک به ترتیب برابر ۲ و ۰.۱ می باشد وارد کنید. هم چنین گزینه Input constant را انتخاب کرده و در کادر مقابل آن عدد ۲.۲ را وارد کرده و OK را بزنید.
Cumulative Distribution Function
Normal with mean = 2 and standard deviation = 0.1
x P( X <= x )
۲.۲ ۰.۹۷۷۲۵۰
تحلیل: احتمال اینکه ضخامت نورد تولید شده حداکثر ۲.۲ باشد برابر ۰.۹۷ می باشد.
برای حل قسمت ب این سوال فقط کافیست به جای گزینه ی Cumulative probability، گزینه ی Inverse Cumulative probability را انتخاب کرده و در کادر مقابل Input constant عدد ۰.۹۷۵ را وارد کرده و OK را بزنید.
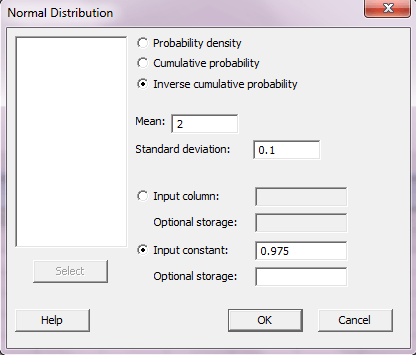
Inverse Cumulative Distribution Function
Normal with mean = 2 and standard deviation = 0.1
P( X <= x ) x
۰.۹۷۵ ۲.۱۹۶۰۰
تحلیل: همانطور که مشاهده می کنید در صورتیکه ضخامت نورد, حداکثر ۲.۱۶ میلی متر باشد با احتمال ۰.۹۷۵ کشف خواهد شد.
قسمت ۳، از آن جاییکه ضخامت نورد توزیع نرمال دارد پس میانگین نمونه این ۹ نمونه نیز توزیع نرمال با میانگین ۲ و انحراف معیار ۹√ /۰.۱ دارد پس می توان برای حل قسمت ۳ احتمال زیر را حل کرد:
p(z ≤ ۲.۱-۲/۰.۰۳) = p(z ≤ ۳)
برای حل احتمال فوق گزینه Cumulative probability را انتخاب کرده و در کادر مقابل Mean و Standard deviation مقدار میانگین و انحراف معیار را که هر یک به ترتیب برابر ۲ و ۰.۰۳ می باشد وارد کنید. هم چنین گزینه Input constant را انتخاب کرده و در کادر مقابل آن عدد ۲.۱ را وارد کرده و OK را بزنید.
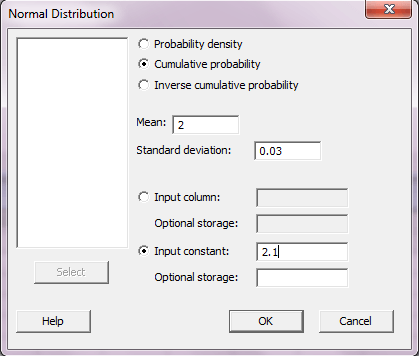
Cumulative Distribution Function
Normal with mean = 2 and standard deviation = 0.03
x P( X <= x )
۲.۱ ۰.۹۹۹۵۷۱
تحلیل: احتمال اینکه میانگین نمونه حداکثر برابر ۲.۱ شود برابر ۰.۹۹ می باشد.
محاسبه احتمال توزیع مربع کای با Minitab
مثال: از یک فرآیند تولید کاغذ یک نمونه ی ۶ تایی تهیه می کنیم. ضخامت کاغذ توزیع نرمال با میانگین ۰ و واریانس ۰ دارد. آن گاه مطلوبست احتمال اینکه:
الف – واریانس نمونه حداکثر۰.۰ باشد؟
ب – واریانس نمونه حداکثر چه قدر باشد تا با احتمال ۲.۶۲ قابل کشف باشد؟
برای محاسبه این احتمال مسیر زیر را دنبال کنید:
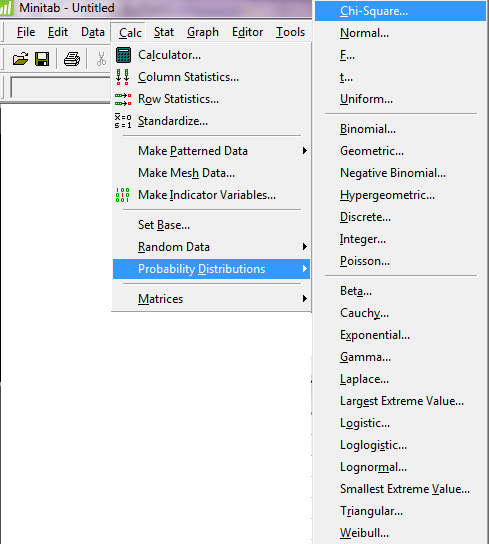
در پنجره Chi-Square distribution گزینه Cumulative probability را انتخاب کرده و در کادر مقابل Degrees of freedom مقدار درجه آزادی که برابر۸ می باشد را وارد کنید و با انتخاب گزینه Input constant عدد ۸.۸ را در مقابل کادر آن وارد کرده و OK را بزنید.
Cumulative Distribution Function
Chi-Square with 8 DF
x P( X <= x )
۸.۸ ۰.۶۴۰۵۵۲
تحلیل: احتمال اینکه واریانس نمونه حداکثر ۱.۱ باشد، ۰.۶۴ می باشد.
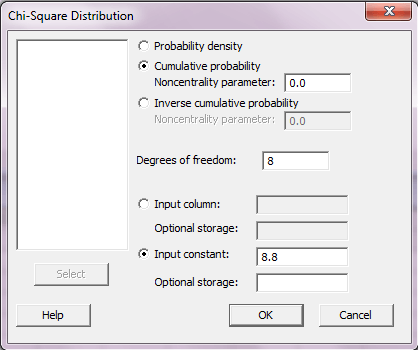
برای حل قسمت ب این سوال کافیست در پنجره Chi-Square distribution , گزینه Inverse cumulative distribution را انتخاب کرده و در کادر مقابل Input constant عدد ۰.۹۵ را وارد کرده و OK را بزنید.
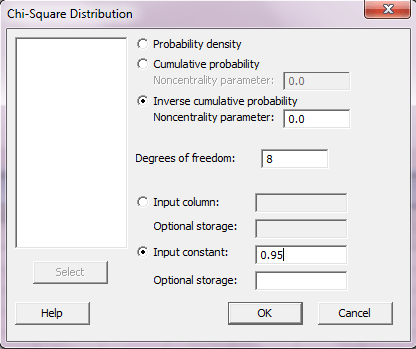
Inverse Cumulative Distribution Function
Chi-Square with 8 DF
P( X <= x ) x
۰.۹۵ ۱۵.۵۰۷۳
محاسبه احتمال توزیع t با Minitab
مثال: فرض کنید یک نمونه ی ۱۰ تایی از یک فرآیند تولید لامپ تهیه کردیم به طوریکه عمر لامپ ها توزیع نرمال با میانگین ۱ سال و انحراف معیار نامعلوم دارند. انحراف معیار نمونه برای این ۱۰ لامپ برابر ۶ ماه می باشد. آن گاه مطلوبست
- احتمال اینکه میانگین نمونه عمر این لامپ ها حداکثر برابر ۰.۲ سال باشد؟
- میانگین نمونه حداکثر چه قدر باشد تا با احتمال حداقل ۲.۶۲ قابل کشف باشند؟
- فرض کنید یک نمونه ی ۰۳ تایی دیگر از این فرآیند تهیه کردیم و انحراف معیار نمونه آن برابر ۵ ماه به دست آمده باشد, احتمال اینکه تفاوت میانگین نمونه از این دو بار نمونه گیری برابر ۰ ماه باشد را به دست آورید؟
برای حل سه قسمت این سوال مسیر زیر را دنبال کنید:
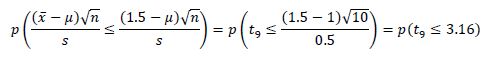
در قسمت ۱ برای محاسبه احتمال در پنجره t distribution گزینه Cumulative probability را انتخاب کرده و در کادر مقابل Degrees of freedom عدد ۹ را وارد کنید و گزینه Input constant را انتخاب کرده و در کادر مقابل آن عدد ۳.۱۶ را وارد کنید و OK را بزنید.
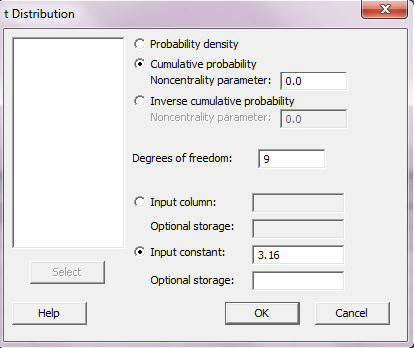
Cumulative Distribution Function
Student’s t distribution with 9 DF
x P( X <= x )
۳.۱۶ ۰.۹۹۴۲۲۵
تحلیل: احتمال اینکه میانگین نمونه این ۱۰ لامپ حداکثر ۱.۵ سال شود برابر ۰.۹۹ می باشد.
برای حل قسمت ۲ این سوال کافیست در پنجره t distribution، گزینه Inverse cumulative distribution را انتخاب کرده و در کادر مقابل Input constant عدد ۰.۹۵ را وارد کرده و OK را بزنید.
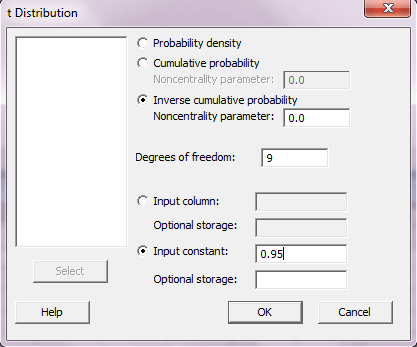
Inverse Cumulative Distribution Function
Student’s t distribution with 9 DF
P( X <= x ) x
۰.۹۵ ۱.۸۳۳۱۱
در قسمت ۳ باید احتمال را محاسبه کنیم. پس برای محاسبه احتمال مورد نظر طبق تصویر زیر عمل کنید.
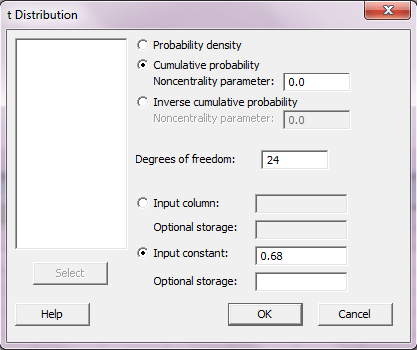
Cumulative Distribution Function
Student’s t distribution with 24 DF
x P( X <= x )
۰.۶۸ ۰.۷۴۸۴۹۴
تحلیل: احتمال اینکه اختلاف میانگین نمونه حداکثر برابر دو ماه شود برابر ۰.۷۴ می باشد.
محاسبه احتمال توزیع F با Minitab
مثال: فرض کنید یک نمونه ی ۱۶ تایی از یک جامعه ی نرمال با واریانس ۱ انتخاب کردیم و یک نمونه ی ۹ تایی نیز از یک جامعه نرمال دیگر با واریانس ۲ انتخاب کردیم. مطلوبست محاسبه احتمال اینکه نسبت واریانس نمونه برای این دو جامعه حداکثر برابر ۱.۵ باشد؟
برای حل این سوال ابتدا مسیر زیر را دنبال کنید:
برای حل این سوال باید احتمال را محاسبه کنیم.گزینه برای حل احتمال (p(F(15,8)≥ ۳ F distribution در پنجره Cumulative probability را انتخاب کرده و در کادر مقابل Numerators Degrees of freedom عدد ۱۵ ودر کادر مقابل denominator degrees of freedom عدد ۸ را وارد کنید و گزینه Input constant را انتخاب کرده و در کادر مقابل آن عدد ۳ را وارد کرده و OK را بزنید.
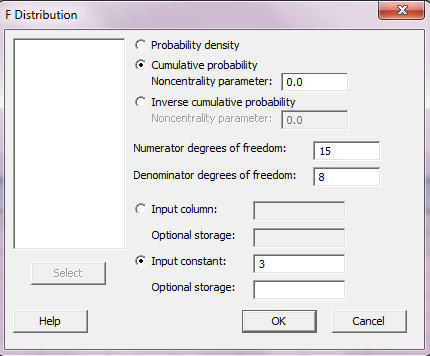
Cumulative Distribution Function
F distribution with 15 DF in numerator and 8 DF in denominator
x P( X <= x )
۳ ۰.۹۳۹۵۳۵
تحلیل: همانطور که مشاهده می کنید احتمال اینکه نسبت دو واریانس نمونه حداکثر برابر ۱.۵ شود برابر ۰.۹۳ می باشد.
پیدا کردن تابع توزیع یک متغیر تصادفی
همواره یکی از مشکلاتی که برای یک تحلیل گر آماری در کلیه زمینه های آمار به وجود می آید این است که نمونه هایی که یک تحلیل گر گردآوری کرده است ، از چه تابع توزیعی پیروی می کند؟به ندرت پیش می آید که متغیر تصادفی شما از تابع توزیع نرمال پیروی کند. لذا همیشه انجام یک آزمون برای اینکه داده ها از چه تابع توزیعی پیروی می کنند، اجتناب ناپذیر است.
معمولا ابزارهای مختلفی برای برازش داده ها وجود دارد. مانند هیستوگرام که از روی شکل توزیع می توان آن را حدس زد یا آزمون فرض نیکویی برازش مربع کای که دقیق تر از هیستوگرام می باشد چون بر اساس روابط آماری داده ها را برازش می کند نه از روی شکل و حدس و گمان, اما ضعفی که این آزمون دارد.
این است که به اندازه نمونه بسیار بالایی نیاز دارد. آزمون دیگر، آزمون کولموگروف اسمیرنف می باشد که ضعف آزمون نیکویی برازش را پوشش داده است و در اندازه نمونه های پایین تر نیز می توان به نتایج مطمئن تری دست یافت
اما بهترین آزمون، آزمون اندرسون دارلینگ می باشد این آزمون قوی ترین آزمون برای برازش داده ها می باشد و در اندازه نمونه های حتی کمتر از ده نیز می توان به نتایج مطمئنی دست یافت. در مورد هر یک از ابزارهای ذکر شده در فصل های آتی توضیحات مفصلی داده شده است. در ادامه آموزش توزیع های احتمالی در مینی تب به بررسی تابع توزیع متغیر تصادفی میپردازیم.
پیدا کردن تابع توزیع یک متغیر تصادفی با Minitab
نرم افزار Minitab قابلیت برازش ۵۸ تابع توزیع پیوسته را با آزمون اندرسون دارلینگ و هم چنین رسم هم زمان طرح احتمال آن ها دارد. در صورتیکه مقدار P-Value از خطای نوع اول آزمون (α) بیشتر شود, بدین معنی می باشد که فرض صفر در آزمون اندرسون دارلینگ قبول می شود. فرض صفر در این آزمون مبنی بر اینکه داده های جمع آوری شده تابع توزیع خاصی دارند می باشد.
از آن جاییکه ممکن است چندین P-Value برای برازش داده ها برای چند توزیع بیش از α شود, آن گاه تابع توزیعی را انتخاب کنید که بیشترین مقدار P-value را داشته باشد .یکی دیگر از روش هایی که Minitab به برازش داده ها می پردازد روش آزمون نسبت درست نمایی (Likelihood ratio test) می باشد, این روش به این صورت است که به مقایسه برازش دو مدل می پردازد.
یکی مدل فرض صفر و دیگر مدل تصمیم گیری. مدل فرض صفر در این آزمون همان تخمین پارامتر به روش درست نمایی در شرایط بزرگ تر تابع توزیع مثلا وقتی سه پارامتر آزاد دارد و مدل تصمیم گیری در شرایط کوچک تر تابع توزیع مثلا وقتی دو پارامتر آزاد دارد می باشد .در صورتیکه مقدار P-Value در این آزمون کمتر از α باشد فرض مبنی بر اینکه تابع توزیع مورد بررسی, تابعی مناسب برای داده های شما می باشد می پذیریم در نظر داشته باشید که اگر چندین P-Value کمتر از α شد, تابع توزیعی را انتخاب کنید که کمترین P-value را داشته باشد.
در نظر داشته باشید که اگر همه ی تابع توزیع ها در این آزمون رد شدند، یا اندازه نمونه خود را افزایش دهید یا اینکه می توان گفت که داده های شما از تابع توزیع تجربی( Empirical distribution ) پیروی می کنند.
مثال : فرض کنید شما برای شرکتی کار می کنید که کارش موزائیک کردن زمین می باشد و شما نگران میزان پایداری موزائیک ها هستید. برای مطمئن شدن از کیفیت محصول شما میزان پایداری را در۱۰ موزائیک در ۱۰ روز اندازه گیری می کنید و داده های زیر به دست می آید. میزان پایداری در موزائیک ها از چه تابع توزیعی پیروی می کنند؟
قدم اول : کاربرگ Tiles.MTW را از منوی File دستور Open worksheet باز کنید.
قدم دوم : مسیر زیر را دنبال کنید.
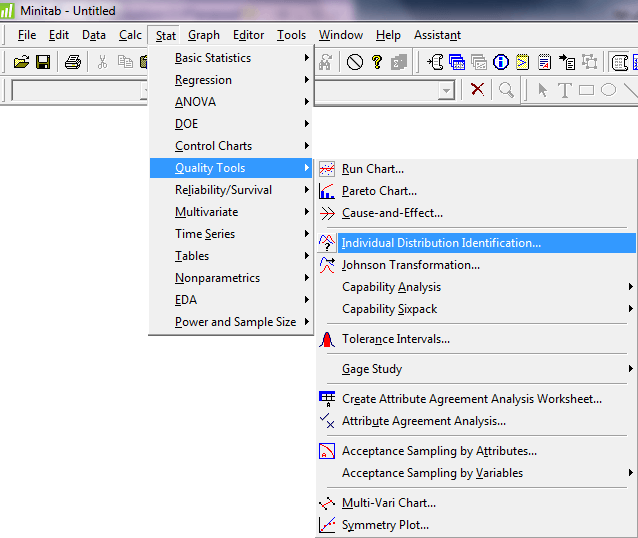
قدم سوم: در قسمت Single columns ستون C1 را وارد کنید.
قدم چهارم : در صورتیکه گزینه ی Use all distributions را بزنید، نرم افزار کلیه ۱۴ تابع توزیع را بروی داده های شما آزمون می کند و در غیر اینصورت گزینه ی Specify را انتخاب کرده و از ۴ تابع توزیعی که نرم افزار در اختیار شما قرار داده هر کدام را به دلخواه انتخاب کنید.حتی می توانید هم زمان هر ۴ تابع توزیع را روی داده هایتان آزمون کنید .
قدم پنجم: به Option رفته و سطح اطمینان(Confidence level (1-α را مشخص کنید.که به طور پیش فرض ۰.۹۵ است و Ok را بزنید.
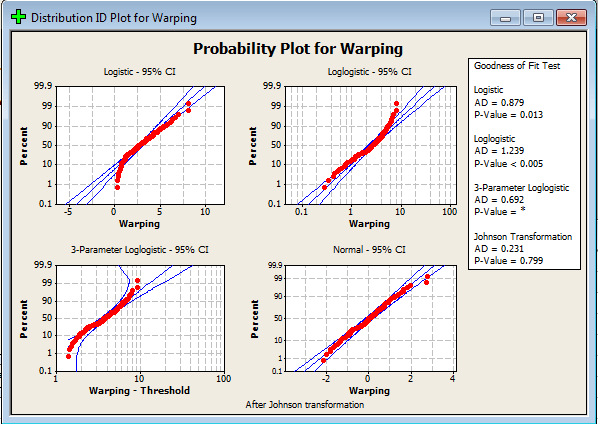
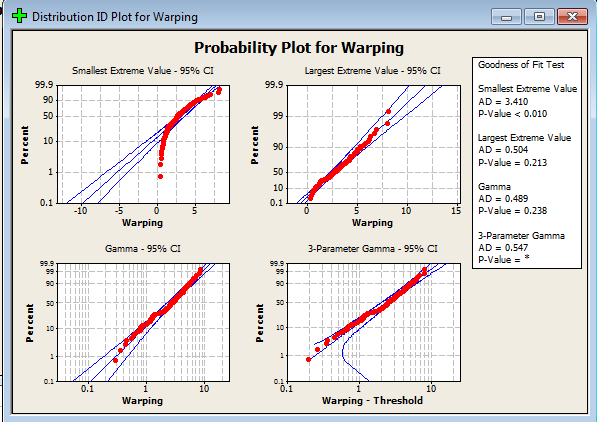
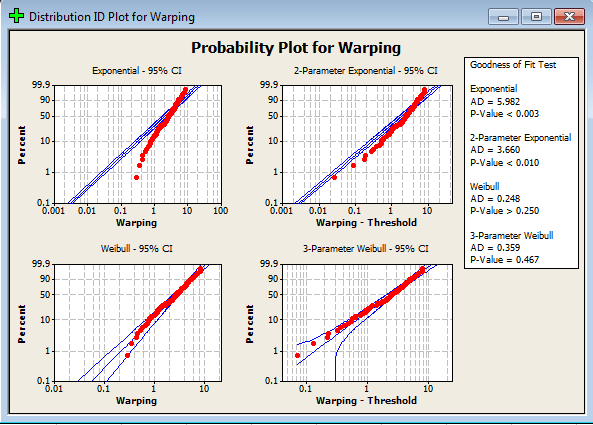
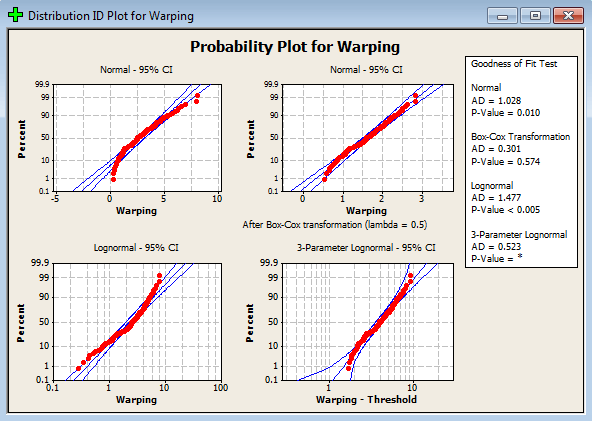
تحلیل: همانطور که مشاهده می کنید مقدار P-Value برای آزمون اندرسون دارلینگ برای تابع توزیع ویبول با سه پارامتر برابر ۰.۴۶ شده و بیشترین مقدار P-value می باشد.
هم چنین داده های جمع آوری شده به خوبی طرح احتمال این تابع توزیع را پوشش دادند, اما بر اساس آزمون نسبت درست نمایی توزیع وایبول با سه پارامتر توزیع مناسبی نمی باشد و توزیع نمای با دو پارامتر می تواند داده های شما را به خوبی پوشش دهد چون مقدار P-value برای این توزیع بر اساس آزمون نسبت درست نمایی برابر صفر شده به همین خاطر Minitab تابع توزیع نمایی را با متوسط ۲.۶۶ (بر اساس تخمین MLE) و برای ۰.۲۵≤ X بهترین توزیع می داند
هر چند آزمون اندرسون دارلینگ این توزیع را رد کرده است و توزیع ویبول با پارامترهای شکل برابر ۱.۵ و مقیاس ۲.۹۹ برای ۰.۲≤ X را مناسب می داند.
خب به پایان یادگیری این بخش از یادگیری نرم افزار مینی تب رسیدیم.
امیدواریم از این مقاله که درباره یادگیری نرم افزار مینی تب در صنایع سافت بود لذت برده باشید. هر سوال و نظری دارید برای ما کامنت بذارید، کمتر از یک روز پاسخ داده میشه 😉






سلام عالی ومفید بود
طریقه محاسبه سطح سیگما و مقدار ppm در نرم افزار چگونه است؟