آموزش رایگان متلب برای مهندسان صنایع | (قسمت سوم)
آموزش رایگان متلب
در ادامه آموزش رایگان متلب برای مهندسان صنایع که یکی از نرم افزار های این رشه میباشد به بررسی موارد زیر خواهیم پرداخت :
- ماتریسهای سه بعدی و یا بالاتر
- ذخیره چند ماتریس در یک ماتریس سه بعدی
- عملیات جبری مقدماتی
- ضرب، تقسیم و توان عنصر به عنصر
- توابع مقدماتی
- توابع نظریه اعداد
- توزیع نرمال
- توابع پرکاربرد آرایه های و ماتریسی

ماتریسهای سه بعدی و یا بالاتر
برای یک ماتریس از لحاظ تعریف برای بعد هیچ محدودیتی وجود ندارد اما عموم ماتریسهایی که ما با آنها سروکار داریم ماتریسهای دو بعدی هستند. در مباحث معمول کمتر به یک ماتریس با بعد بالاتر نیاز پیدا خواهیم کرد مگر حالت خاصی که بخواهیم تعدادی ماتریس را با نام یکسان ذخیره کنیم اما در بحث های مقداری پیشرفته تر ماتریسهای با مرتبه ۳ مواردی هستند به آشنایی و کار با آنها نیاز داریم.
تعریف و فراخوانی ماتریس مرتبه ۳
یک ماتریس مرتبه سه را می توانیم بصورت عنصر به عنصر تعریف کنیم و یا اینکه با ماتریس های با سایز یکسان که در بعد سوم کنار هم چیده می شوند آن را ایجاد کنیم. برای راحتی می توانیم چنین تصور کنیم که چندین صفحه در فضا به موازات هم چیده می شوند. شکل های help متلب در این زمینه بسیار گویا است و ما همین شکل ها را در ادامه می آوریم.
ماتریس دوبعدی
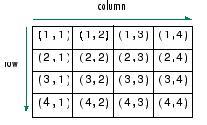
ماتریس سه بعدی
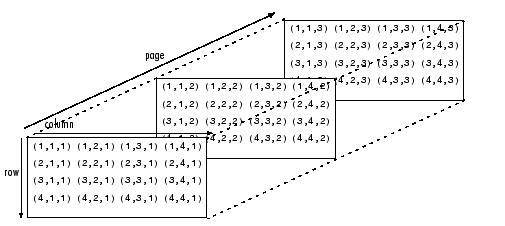
برای نمونه به نحوه ی تعریف جایگاه عناصر در ماتریس سه بعدی زیر توجه کنید
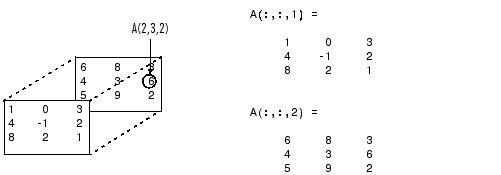
مثال های زیر چند نمونه از تعریف ماتریس سه بعدی هستند
>> A(1,1,1)=5;A(1,1,2)=8;A(1,2,1)=10;A(1,2,2)=2; >> A A(:,:,1) = ۵ ۱۰ A(:,:,2) = ۸ ۲ >> I=ones(3,4,2) I(:,:,1) = ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ I(:,:,2) = ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱
برای آشنایی با فراخوانی در ماتریس های سه بعدی مثالهای زیر را دنبال کنید.
>> U=rand(3,4,2) U(:,:,1) = ۰.۱۶۸۱ ۰.۸۰۹۹ ۰.۰۳۰۹ ۰.۴۱۰۴ ۰.۰۵۲۶ ۰.۹۷۹۳ ۰.۶۵۳۱ ۰.۱۶۹۸ ۰.۵۸۹۳ ۰.۴۶۳۱ ۰.۱۷۷۰ ۰.۳۶۱۵ U(:,:,2) = ۰.۹۴۴۶ ۰.۹۳۸۱ ۰.۶۴۵۵ ۰.۳۰۶۲ ۰.۲۱۴۲ ۰.۶۶۱۷ ۰.۸۵۳۰ ۰.۵۸۱۴ ۰.۳۶۶۲ ۰.۹۸۳۹ ۰.۱۳۳۷ ۰.۶۰۳۱ >> U(1,2,2) ans = ۰.۹۳۸۱ >> U(3,4,2) ans = ۰.۶۰۳۱ >> U(2,3,2) ans = ۰.۸۵۳۰ >> U(2,:,2) ans = ۰.۲۱۴۲ ۰.۶۶۱۷ ۰.۸۵۳۰ ۰.۵۸۱۴ >> U(1,:,2) ans = ۰.۹۴۴۶ ۰.۹۳۸۱ ۰.۶۴۵۵ ۰.۳۰۶۲ >> U(:,1,2) ans = ۰.۹۴۴۶ ۰.۲۱۴۲ ۰.۳۶۶۲ >> U(:,3,1) ans = ۰.۰۳۰۹ ۰.۶۵۳۱ ۰.۱۷۷۰ >> U(1,3,:) ans(:,:,1) = ۰.۰۳۰۹ ans(:,:,2) = ۰.۶۴۵۵ >> U(:,:,1) ans = ۰.۱۶۸۱ ۰.۸۰۹۹ ۰.۰۳۰۹ ۰.۴۱۰۴ ۰.۰۵۲۶ ۰.۹۷۹۳ ۰.۶۵۳۱ ۰.۱۶۹۸ ۰.۵۸۹۳ ۰.۴۶۳۱ ۰.۱۷۷۰ ۰.۳۶۱۵
پس از آشنایی با فراخوانی، مقداردهی ماتریس های سه بعدی دیگر کار دشواری نیست
ذخیره چند ماتریس در یک ماتریس سه بعدی
یکی از مواردی که عموما در کار با ماتریس های سه بعدی به آن برخورد می کنیم ذخیره ی چند ماتریس دوبعدی در یک ماتریس سه بعدی است
برای مثال فرض کنید میخواهیم سه ماتریس ۵×۴، Aو B و C را که بصورت زیر تعریف شدهاند را در یک ماتریس سه بعدی ذخیره کنیم.
>> A=zeros(4,5); >> B=ones(4,5); >> C=5*ones(4,5);
با روش زیر این ماتریس ها را در ماتریس سه بعدی ذخیره می کنیم.
>> D(:,:,1)=A; >> D(:,:,2)=B; >> D(:,:,3)=C; >> whos Name Size Bytes Class Attributes ۴۹ A 4x5 160 double B 4x5 160 double C 4x5 160 double D 4x5x3 480 double
D یک ماتریس سه بعدی است
>> D(:,:,1) ans = ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ است A همان >> D(:,:,3) ans = ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ ۵ است C همان >> D(1,:,:) ans(:,:,1) = ۰ ۰ ۰ ۰ ۰ ans(:,:,2) = ۱ ۱ ۱ ۱ ۱ ans(:,:,3) = ۵ ۵ ۵ ۵ ۵ ترکیبی از ماتریسهاست
عکس این کار نیز ذخیره ی عناصر یک ماتریس سه بعدی در چند ماتریس دوبعدی است، برای مثال فرض کنید همین ماتریس D را می خواهیم در چند ماتریس دوبعدی ذخیره کنیم.
>> A1=D(:,:,1); >> A2=D(:,:,2); >> A3=D(:,:,3); >> A2 A2 = ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱ ۱
اگر بخواهیم عبارت را بصورت زیر بنویسیم
>> A1=D(1,:,:) A1(:,:,1) = ۰ ۰ ۰ ۰ ۰ A1(:,:,2) = ۱ ۱ ۱ ۱ ۱ A1(:,:,3) = ۵ ۵ ۵ ۵ ۵
با توجه به اینکه (:,:,D(1 یک ماتریس سه بعدی است، A1 نیز یک ماتریس سه بعدی خواهد شد که با آنچه ما می خواستیم متفاوت خواهد بود.
گهگاهی نیز در ذخیره ماتریس ها در یک ماتریس سه بعدی ممکن است با نوشتن دستور بصورت اشتباه به خطای زیر برخورد کنیم
>> D(4,:,:)=A ??? Subscripted assignment dimension mismatch. که در این موارد خطا به علت یکسان نبودن ابعاد طرفین تساوی رخ داده است
صورت صحیح عبارت بالا بشکل زیر است که قبلا ذکر شد
>> D(:,:,4)=A
عملیات جبری مقدماتی
مقدمه
در ادامه آموزش رایگان متلب ساده ترین اعمال جبری جمع و تفریق هستند. تنها نکته ای که وجود دارد این است که در مورد بردارها و یا ماتریس ها در صورت جمع یا تفریق هردو ماتریس (و یا بردار) باید طول یکسانی داشته باشند. استثنا درمورد جمع آرایه ها و یا ماتریس ها با یک عدد است که در این صورت همه ی عناصر با عدد جمع می شوند. ضرب ماتریسی نیز عمل آشنایی است.
>> 2+2 ans = ۴ >> 2-2 ans = ۰ >> 2*2 ans = ۴ >> 2/2 ans = ۱ >> 10/5 ans = ۲ >> 10\5 ۵/ تقسیم از راست معادل ۱۰ ans = ۰.۵۰۰۰ >> 2^10 ans = ۱۰۲۴ >> 2^0.5 √ معادل ۲ ans = ۱.۴۱۴۲ >> sqrt(2) تابع رادیکال است sqrt() ans = ۱.۴۱۴۲ >> 2^-1 ans = ۰.۵۰۰۰ >>A=[1 2 3;4 5 6; 7 8 9];B=[10 20 30;40 50 60; 70 80 90]; >>a=[1 2 3];b=[10 20 30]; >>a+b ans = ۱۱ ۲۲ ۳۳ >>A+B ans = ۱۱ ۲۲ ۳۳ ۴۴ ۵۵ ۶۶ ۷۷ ۸۸ ۹۹ >>a+6 ans = ۷ ۸ ۹ >>B+.2 ans = ۱۰.۲۰۰۰ ۲۰.۲۰۰۰ ۳۰.۲۰۰۰ ۴۰.۲۰۰۰ ۵۰.۲۰۰۰ ۶۰.۲۰۰۰ ۷۰.۲۰۰۰ ۸۰.۲۰۰۰ ۹۰.۲۰۰۰ >> a/2 ans = ۰.۵۰۰۰ ۱.۰۰۰۰ ۱.۵۰۰۰ >> 2*a ans = ۲ ۴ ۶ >> 10*A ans = ۱۰ ۲۰ ۳۰ ۴۰ ۵۰ ۶۰ ۷۰ ۸۰ ۹۰ >> A/5 ans = ۰.۲۰۰۰ ۰.۴۰۰۰ ۰.۶۰۰۰ ۰.۸۰۰۰ ۱.۰۰۰۰ ۱.۲۰۰۰ ۱.۴۰۰۰ ۱.۶۰۰۰ ۱.۸۰۰۰ >> A+B ans = ۱۱ ۲۲ ۳۳ ۴۴ ۵۵ ۶۶ ۷۷ ۸۸ ۹۹ >> A*A ضرب ماتریسی ans = ۳۰ ۳۶ ۴۲ ۶۶ ۸۱ ۹۶ ۱۰۲ ۱۲۶ ۱۵۰ >> A^2 A^2 ≡ A*A ans = ۳۰ ۳۶ ۴۲ ۶۶ ۸۱ ۹۶ ۱۰۲ ۱۲۶ ۱۵۰ >> A^3 A^3 ≡ A*A*A ans = ۴۶۸ ۵۷۶ ۶۸۴ ۱۰۶۲ ۱۳۰۵ ۱۵۴۸ ۱۶۵۶ ۲۰۳۴ ۲۴۱۲ >> C=[1 2;3 4]; >> C^-1 ans = -۲.۰۰۰۰ ۱.۰۰۰۰ ۱.۵۰۰۰ -۰.۵۰۰۰ ( است (در این خصوص در زیرفصل مربوطه صحبت خواهد شد A معادل معکوس ماتریس >> a*A ضرب بردار در ماتریس ans = ۳۰ ۳۶ ۴۲ >> A*B ans = ۳۰۰ ۳۶۰ ۴۲۰ ۶۶۰ ۸۱۰ ۹۶۰ ۱۰۲۰ ۱۲۶۰ ۱۵۰۰
- در جمع (و یا ضرب ، تفریق و تقسیم) آرایه یا ماتریس با یک عدد همه عناصر با آن عدد جمع (و یا ضرب ، تفریق ، و تقسیم) می شوند
ترانهاد
عملگر’ عملگر ترانهاده می باشد و برای یک ماتریس با عناصر حقیقی ترانهاده ی ماتریس را بدست می دهد ترانهاد یک بردار سطری یک بردار ستونی و همینطور ترانهاد یک بردار ستونی بردار سطری است. اگر عناصر ماتریس مختلط باشند عملگر فوق علاوه بر ترانهادگیری بجای عناصر ماتریس مزدوج مختلط آنها را نیز حساب می کند. برای اجتناب از این امر از عملگر .’ استفاده می کنیم که در هر دو صورت عناصر حقیقی و یا مختلط فقط ترانهاد را بدست می دهد.
>> a=1:4; >> b=[1-3i 1+8i 5-6i 7+7i]; >> a a = ۱ ۲ ۳ ۴ >> a' ans = ۱۲۳۴ >> transpose(a) تابع ترانهاد که معادل عملگر میباشد ans = ۱۲۳۴ >> a.' ans = ۱۲۳۴ دو عملگر پرایم و دات پرایم برای آرایههای حقیقی معادلاند >> b=[1-3i ;1+8i; 5-6i ;7+7i] b = ۱.۰۰۰۰ - ۳.۰۰۰۰i ۱.۰۰۰۰ + ۸.۰۰۰۰i ۵.۰۰۰۰ - ۶.۰۰۰۰i ۷.۰۰۰۰ + ۷.۰۰۰۰i >> b' ترانهد علاوهی مزدوج مختلط ans = ۱.۰۰۰۰ + ۳.۰۰۰۰i 1.0000 - 8.0000i 5.0000 + 6.0000i ۷.۰۰۰۰ - ۷.۰۰۰۰i >> b.' فقط ترانهاد ans = ۱.۰۰۰۰ - ۳.۰۰۰۰i 1.0000 + 8.0000i 5.0000 - 6.0000i ۷.۰۰۰۰ + ۷.۰۰۰۰i >> A=randint(4,4,[-10 10]) یک ماتریس دلخواه A = -۵ ۴ -۱ -۷ -۱۰ -۴ -۲ ۰ -۸ ۹ ۶ -۱ ۷ -۱۰ ۶ ۳ >> A' ans = -۵ -۱۰ -۸ ۷ ۴ -۴ ۹ -۱۰ -۱ -۲ ۶ ۶ -۷ ۰ -۱ ۳ >> a*a' ans = ۳۰ >> b*b' ans = ۳۰۰۰
ضرب، تقسیم و توان عنصر به عنصر
در ادامه آموزش رایگان متلب وقتی دو ماتریس را با هم جمع می کنیم هر عنصر با عنصر متناظر خود جمع می شود اگر بخواهیم چنین موردی نیز برای ضرب داشته باشیم یعنی اینکه برای مثال در ضرب دو ماتریس تنها عناصر متناظر، در هم ضرب شوند می توانیم از ضرب عنصر به عنصر تعریف شده در متلب استفاده کنیم که با نماد *. (می توانیم بخوانیم دات ضرب) نشان داده می شود. شبیه این عمل را برای تقسیم و توان نیز داریم /. (می توانیم بخوانیم دات تقسیم) و ^. (می توانیم بخوانیم دات توان)
>> a=1:4 a = ۱ ۲ ۳ ۴ >> b=[10 20 30 40]; b = ۱۰ ۲۰ ۳۰ ۴۰ >> a.*b ans = ۱۰ ۴۰ ۹۰ ۱۶۰ >> a*b ابعاد متناسب نیست ??? Error using ==> mtimes Inner matrix dimensions must agree. >> a./b ans = ۰.۱۰۰۰ ۰.۱۰۰۰ ۰.۱۰۰۰ ۰.۱۰۰۰ >> b./a ans = ۱۰ ۱۰ ۱۰ ۱۰ >> b^a تعریف نشده ??? Error using ==> mpower At least one operand must be scalar. >> b.^a ans = ۱۰ ۴۰۰ ۲۷۰۰۰ ۲۵۶۰۰۰۰ >> b^2 ??? Error using ==> mpower Matrix must be square. >> b.^2 ans = ۱۰۰ ۴۰۰ ۹۰۰ ۱۶۰۰ >> b.^0.5 ans = ۳.۱۶۲۳ ۴.۴۷۲۱ ۵.۴۷۷۲ ۶.۳۲۴۶ >> 2.^a ans = ۲ ۴ ۸ ۱۶ >> 2.^b ans = ۱.0e+012 * همهی عناصر باید در این عدد ضرب شوند ۰.۰۰۰۰ ۰.۰۰۰۰ ۰.۰۰۱۱ ۱.۰۹۹۵ >> 3.^a ans = ۳ ۹ ۲۷ ۸۱ >> 2.^[0:5] ans = ۱ ۲ ۴ ۸ ۱۶ ۳۲ >> [0:5].^2 ans = ۰ ۱ ۴ ۹ ۱۶ ۲۵ >> A=randint(4,4,[-10 10]) A = ۴ ۳ ۱۰ ۵ ۵ -۷ -۳ -۵ -۵ -۸ ۲ ۰ ۴ ۰ -۶ ۴ >> B=magic(4) B = ۱۶ ۲ ۳ ۱۳ ۵ ۱۱ ۱۰ ۸ ۹ ۷ ۶ ۱۲ ۴ ۱۴ ۱۵ ۱ >> A.*B ans = ۶۴ ۶ ۳۰ ۶۵ ۲۵ -۷۷ -۳۰ -۴۰ -۴۵ -۵۶ ۱۲ ۰ ۱۶ ۰ -۹۰ ۴ >> A./B ans = ۰.۲۵۰۰ ۱.۵۰۰۰ ۳.۳۳۳۳ ۰.۳۸۴۶ ۱.۰۰۰۰ -۰.۶۳۶۴ -۰.۳۰۰۰ -۰.۶۲۵۰ -۰.۵۵۵۶ -۱.۱۴۲۹ ۰.۳۳۳۳ ۰ ۱.۰۰۰۰ ۰ -۰.۴۰۰۰ ۴.۰۰۰۰ >> A.^2 ans = ۱۶ ۹ ۱۰۰ ۲۵ ۲۵ ۴۹ ۹ ۲۵ ۲۵ ۶۴ ۴ ۰ ۱۶ ۰ ۳۶ ۱۶ >> B.^0.5 است sqrt(B) معادل ans = ۴.۰۰۰۰ ۱.۴۱۴۲ ۱.۷۳۲۱ ۳.۶۰۵۶ ۲.۲۳۶۱ ۳.۳۱۶۶ ۳.۱۶۲۳ ۲.۸۲۸۴ ۳.۰۰۰۰ ۲.۶۴۵۸ ۲.۴۴۹۵ ۳.۴۶۴۱ ۲.۰ ۳.۷۴۱۷ ۳.۸۷۳۰ ۱.۰۰۰۰
توابع مقدماتی
توابع مثلثاتی
در این فصل سعی در معرفی تعدادی از پرکاربردترین توابع موجود در متلب داریم که البته در فصول فبل با تعدادی از آنها آشنا شده ایم
>> a=[pi/2 .2 pi/5 -.2] a = ۱.۵۷۰۸ ۰.۲۰۰۰ ۰.۶۲۸۳ -۰.۲۰۰۰ >> A=[pi/2 pi;-pi/3 pi/6 ] A = ۱.۵۷۰۸ ۳.۱۴۱۶ -۱.۰۴۷۲ ۰.۵۲۳۶ >> rad2deg(pi) ans = ۱۸۰ >> pi*(180/pi) ans = ۱۸۰ >> deg2rad(90) ans = ۱.۵۷۰۸ >> 90*(pi/180) ans = ۱.۵۷۰۸ >> sin(pi) ans = ۱.۲۲۴۶e-016 >> sin(pi/4) ans = ۰.۷۰۷۱ >> sin(a) ans = ۱.۰۰۰۰ ۰.۱۹۸۷ ۰.۵۸۷۸ -۰.۱۹۸۷ >> sin([0:.2:1]*pi) ans = ۰ ۰.۵۸۷۸ ۰.۹۵۱۱ ۰.۹۵۱۱ ۰.۵۸۷۸ ۰.۰۰۰۰ >> sin(A) ans = ۱.۰۰۰۰ ۰.۰۰۰۰ -۰.۸۶۶۰ ۰.۵۰۰۰ >> cos(pi/2) ans = ۶.۱۲۳۲e-017 با تقریب خوبی صفر است >> tan(pi/6) ans = ۰.۵۷۷۴ >> cot(pi/4) ans = ۱.۰۰۰۰
توابع مثلثاتی با آرگومان ورودی بر حسب درجه
>> sind(30) ans = ۰.۵۰۰۰
>> sin(30*(pi/180)) sind معادل کار ans = ۰.۵۰۰۰ >> sind(90) ans = ۱ >> cosd(180) ans = -۱
معکوس توابع مثلثاتی
>> asin(.5) ans = ۰.۵۲۳۶ >> acos(0) ans = ۱.۵۷۰۸ >> asin(3) ans = ۱.۵۷۰۸ - ۱.۷۶۲۷i >> atan(2) ans = ۱.۱۰۷۱ >> acot(1) ans = ۰.۷۸۵۴ >> asin(3) برای اعداد حقیقی سینوس بین ۱- و ۱ است ans = ۱.۵۷۰۸ - ۱.۷۶۲۷i
معکوس توابع مثلثاتی با خروجی درجه
>> asind(.5) ans = ۳۰.۰۰۰۰ >> asin(.5)*(180/pi) را انجام میدهد asind معادل کار ans = ۳۰.۰۰۰۰ >> asind(1/sqrt(2)) ans = ۴۵.۰۰۰۰ >> asind(1) ans = ۹۰ >> atand(1) ans = ۴۵
توابع نمایی و لگاریتمی
(exp (x: مقدار ex را محاسبه می کند.
>> a=[pi/2 .2 pi/5 -.2] a = ۱.۵۷۰۸ ۰.۲۰۰۰ ۰.۶۲۸۳ -۰.۲۰۰۰ >> A=[pi/2 pi;-pi/3 pi/6 ] A = ۱.۵۷۰۸ ۳.۱۴۱۶ -۱.۰۴۷۲ ۰.۵۲۳۶ >> exp(3) ans = ۲۰.۰۸۵۵ >> e^3 ??? Undefined function or variable 'e'. چه باشد جواب متفاوت خواهد بود e این فرم نوشتار برای تابع صحیح نیست و بسته به اینکه >> e=10;e^3 ۱۰^۳ ans = ۱۰۰۰ >> exp(-3) ans = ۰.۰۴۹۸ >> exp(-2:4) ans = ۰.۱۳۵۳ ۰.۳۶۷۹ ۱.۰۰۰۰ ۲.۷۱۸۳ ۷.۳۸۹۱ ۲۰.۰۸۵۵ ۵۴.۵۹۸۲ >> exp(a) ans = ۴.۸۱۰۵ ۱.۲۲۱۴ ۱.۸۷۴۵ ۰.۸۱۸۷ >> exp(A) ans = ۴.۸۱۰۵ ۲۳.۱۴۰۷ ۰.۳۵۰۹ ۱.۶۸۸۱ >> 2^4 ans = ۱۶ >> 2.^A ans = ۲.۹۷۰۷ ۸.۸۲۵۰ ۰.۴۸۳۹ ۱.۴۳۷۵
توابع لگاریتمی
- (log(x: لگاریتم طبیعی (Ln(x
- (log10(x: لگاریتم مبنای ۱۰
- (log2(x: لگاریتم مبنای ۲
>> log10(5) ans = ۰.۶۹۹۰ >> log10(10) ans = ۱ >> log10(10^4) ans = ۴ *>> log10(-2) ans = ۰.۳۰۱۰ + ۱.۳۶۴۴i >> log(10) ans = ۲.۳۰۲۶ >> log(3) ans = ۱.۰۹۸۶ >> log(exp(8)) ans = ۸ >> log2(5) ans = ۲.۳۲۱۹ >> log2(2^4) ans = ۴
توابع هیپربولیک
>> sinh(.2) ans = ۰.۲۰۱۳ >> tanh(.6) ans = ۰.۵۳۷۰ >> asinh(5) ans = ۲.۳۱۲۴ >> atanh(.8) ans = ۱.۰۹۸۶
توابع نظریه اعداد
جزء صحیح و گرد کردن
در ادامه آموزش رایگان متلب توابع معروف برای قسمت صحیح اعداد و گردکردن اعداد توابع زیراند
(floor(x: جزء صحیح x
(ceil(x: گرد کردن به سمت عدد صحیح بزرگتر
(fix(x: قسمت صحیح
(round(x: گرد کردن بسمت عدد صحیح نزدیکتر
>> floor(2.6) ans = ۲ >> floor(-2.6) ans = -۳ >> fix(-2.6) ans = -۲ >> ceil(1.1) ans = ۲ >> round(1.2) ans = ۱ >> round(1.8) ans = ۲
(rem(a,b: باقیمانده تقسیم a به b
>> rem(15,7) ans = ۱ >> rem(15.3,7) ans = ۱.۳۰۰۰
توابع مختلف دیگر از نظریه اعداد
(primes(n: اعداد اول کوچکتر از n را لیست می کند
(isprime(a: برسی می کند که آیا a اول است (۱) یا خیر (۰)
(n! : factorial(n
(a: factor(a را به عوامل اول تجزیه می کند
(num , den] = rat(a]: عدد a را بصورت کسری تبدیل می کند
(lcm(a,b: ک.م.م
(gcm(a,b: ب.م.م
(nchoosek(n,k: انتخاب k شی از n شی
(perms(x: تمام جایگشت های درایه های x
>> primes(10) ans = ۲ ۳ ۵ ۷ >> primes(20) ans = ۲ ۳ ۵ ۷ ۱۱ ۱۳ ۱۷ ۱۹ >> isprime(20) ans = ۰ >> isprime(17) ans = ۱ >> factorial(4) ans = ۲۴ >> factor(50) ans = ۲ ۵ ۵ >> factor(16) ans = ۲ ۲ ۲ ۲ >> [num,den]=rat(.365) num = ۷۳ den = ۲۰۰ >> num/den ans = ۰.۳۶۵۰ >> [num,den]=rat(pi) num = ۳۵۵ den = ۱۱۳ >> num/den ans = ۳.۱۴۱۶ >> lcm(6,8) ans = ۲۴ >> gcd(6,8) ans = ۲ >> perms([2 3 7]) ans = ۷ ۳ ۲ ۷ ۲ ۳ ۳ ۷ ۲ ۳ ۲ ۷ ۲ ۳ ۷ ۲ ۷ ۳ >> n=7;k=3; >> nchoosek(n,k) ans = ۳۵ >> factorial(n)/(factorial(k)*factorial(n-k)) ans = ۳۵
چند تابع پرکاربرد دیگر
تابع سینک
تابع sinc از توابع معروف در ریاضیات مهندسی و برق است
>> sinc(0) ans = ۱ >> sinc(1) sinc(n)= عدد صحیح ۰ n ans = ۳.۸۹۸۲e-017 >> sinc(2) ans = -۳.۸۹۸۲e-017 >> sinc(.1) ans = ۰.۹۸۳۶
توزیع نرمال
تولید رشته ای از اعداد با توزیع نرمال
(randn(1) : normrdn(mu,sigma یک عدد تصادفی با توزیع نرمال میانگین mu و واریانس sigma تولید می کند. حال اگر بخواهیم یک ماتریس n×m از اعداد تصادفی با توزیع نرمال داشته باشیم از (normrnd(mu,signa,n,m استفاده می کنیم
(normcdf(x,mu, sigma: احتمال اینکه مقدار متغیر تصادفی با توزیع نرمال با میانگین mu و واریانس sigma از x کمتر باشد
>> mu=0;sigma=1; >> n=normrnd(mu,sigma,1) n = ۰.۵۳۷۷ >> n=normrnd(mu,sigma,1) n = ۱.۸۳۳۹ >> n=normrnd(mu,sigma,1,5) ۱ از اعداد تصادفی با توزیع نرمال و میانگین و واریانس مشخص * آرایه ۵ n = -۲.۲۵۸۸ ۰.۸۶۲۲ ۰.۳۱۸۸ -۱.۳۰۷۷ -۰.۴۳۳۶ >> P = normcdf(1,mu,sigma) کمتر از ۱ باشد x احتمال اینکه P = ۰.۸۴۱۳ >> P = normcdf(3,mu,sigma) کمتر از ۳ باشد x احتمال اینکه P = ۰.۹۹۸۷ >> P = normcdf([1 3],mu,sigma) P = ۰.۸۴۱۳ ۰.۹۹۸۷ >> P(2)-P(1) بین ۱ و ۳ باشد x احتمال اینکه ans = ۰.۱۵۷۳
در ادامه آموزش رایگان متلب (normspec([x1 x2],mu,sigma: احتمال اینکه متغیر تصادفی با میانگین mu و واریانس sigma بین x1 و x2 باشد همراه با نمودار توزیع تجمعی بسیار گویا
احتمال اینکه یک عدد تصادفی با توزیع نرمال استاندارد بین ۲- و ۲ باشد چقدر است؟
>> mu=0;sigma=1; >> P = normcdf([-2 2],mu,sigma) P = ۰.۰۲۲۸ ۰.۹۷۷۲ >> P(2)-P(1) ans = ۰.۹۵۴۵
>> mu=0;sigma=1; >> p=normspec([-2 2],mu,sigma) p = ۰.۹۵۴۵
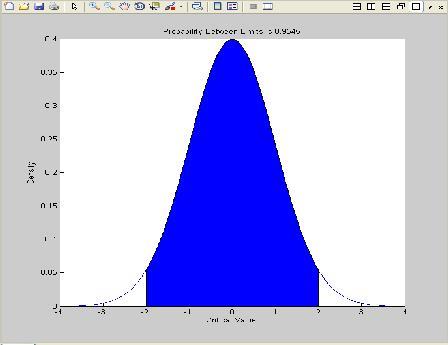
(x = norminv(p,mu,sigma : مقدار x را حساب می کند که بازای آن توزیع تجمعی برابر p شود یعنی:
x : (X ‹ x)=p
این تابع، تابع معکوس توزیع تجمعی است.
محل ۹۰% توزیع تجمعی نرمال میانگین صفر و واریانس یک در کجا قرار دارد؟
>> x=norminv(.9,0,1) x = ۱.۲۸۱۶
بازه ای متقارن حول صفر که ۹۵% مقادیر توزیع نرمال استاندارد در آن قرار دارد را پیدا کنید.
>> p=[.025 .975] p = ۰.۰۲۵۰ ۰.۹۷۵۰ >> p(2)-p(1) ans = ۰.۹۵۰۰ >> x = norminv(p,0,1) x = -۱.۹۶۰۰ ۱.۹۶۰۰
توابع پرکاربرد آرایه های و ماتریسی
اندازه و کمینه ی ماتریس
(length(a: طول بردار a را بدست می دهد
(size(A: سایز ماتریس را نشان می دهد
(numel(A: نتیجه عددی است که برابر تعداد درایه های A است
وقتی می گوییم اندازه ی یک ماتریس ۳×۲ است یعنی تعداد سطرها ۲ و تعداد ستونها ۳ است از آنجا که تعداد سطرها را در ابتدا و تعداد ستونها را در مرتبه دوم ذکر می کنیم این قرارداد را ذکر می کنیم بعد اول سطر، و بعد دوم ستون باشد ممکن است ابعاد دیگری هم داشته باشیم. این قرارداد در بسیاری از موارد در فراخوانی دستورها می تواند به ما کمک کند.
>> A=zeros(5,8); >> B=rand(12,4); >> c=ones(1,7); >> d=ones(4,1); >> length(c) ans = ۷ >> length(d) ans = ۴ >> size(A) ans = ۵ ۸ >> size(B) ans = ۱۲ ۴ >> [m,n]=size(A) m = ۵ n = ۸ >> [m,n]=size(c) m = ۱ n = ۷ >> x=size(A) یک بردار سطری به طول دو است x x = ۵ ۸ >> m*n ans = ۷ >> numel(A) number of elements ans = ۴۰ >> numel(B) ans = ۴۸ >> numel(c) ans = ۷ >> size(A,1) ( تعداد عناصر بعد ۱ (تعداد سطر ها ans = ۵ >> size(A,2) ( تعداد عناصر بعد ۲ (تعداد ستون ها ans = ۸ >> size(B,1) ans = ۱۲ >> size(B,2) ans = ۴
آموزش رایگان برای شما : آموزش MATLAB برای صنایع
(min(a: برای حالتی که a یک بردار باشد این دستور کمینه مقدار این بردار را بدست می دهد و در صورتی که x یک ماتریس باشد تابع min مقدار کمینه ی هر یک از ستون ها را حساب می کند و خروجی یک بردار سطری خواهد بود که هر عنصر نشان دهنده ی مقدار کمینه ی ستون متناظر است. این دستور صورتهای دیگر فراخوانی دارد که در مثال ها آمده است.
(max(a: با کارکردی مشابه دستور (min(a مقدار بیشینه را بدست می دهد
>> min(1,4) مقدار کمینه از بین ۱ و ۴ ans = ۱ >> max(1,4) ans = ۴ >> a1=7;a2=4;max(a1,a2) ans = ۷ >> a = [1 2 3 4 5 6 7]; >> max(a,4) و ۴ a مقدار بیشینه بین درایههای ans = ۴ ۴ ۴ ۴ ۵ ۶ ۷ >> min(a,4) ans = ۱ ۲ ۳ ۴ ۴ ۴ ۴ >> min(a,2) ans = ۱ ۲ ۲ ۲ ۲ ۲ ۲ >> a=[1 5 20 -5 -6 8 -25 9 10 3] a = ۱ ۵ ۲۰ -۵ -۶ ۸ -۲۵ ۹ ۱۰ ۳ >> b = randint(1,10,20) یک آرایهی تصادفی b = ۱۶ ۱۸ ۲ ۱۸ ۱۲ ۱ ۵ ۱۰ ۱۹ ۱۹ >> min(a) a مقدار کمینهی ans = -۶ >> min(b) ans = ۱ >> min(a,b) ans = ۱ ۵ ۲ -۵ -۶ ۱ -۲۵ ۹ ۱۰ ۳ با دو ورودی ، حاصل یک بردار با طول یکسان با بردارهای ورودی و عناصر کمینهی بین دو ورودی min فراخوانی >> max(a,b) ans = ۱۶ ۱۸ ۲۰ ۱۸ ۱۲ ۸ ۵ ۱۰ ۱۹ ۱۹ >> [me ma]=min(a) با دو خروجی مقدار کمینه و مکان عنصر کمینه min فراخوانی دستور me = مقدار -۶ ma = مکان ۵ عنصر پنجم کمینه مقدار را دارد تعریف نام متغیر های خروجی بعلت مشابهت با نام فارسی بوده و اختیاری است >> [me ma]=min(b) me = ۱ ma = ۶ >> [me ma]=max(a) me = ۲۰ ma = ۳ >> [me ma]=min(a) me = -۶ ma = ۵ >> A=randint(4,5,50) A = ۷ ۴۰ ۳۹ ۴۲ ۳۷ ۴۸ ۷ ۴۷ ۴۶ ۱۹ ۴۷ ۲۱ ۳۲ ۳۳ ۳۲ ۲۴ ۴۵ ۱ ۳۷ ۸ >> min(A) مقدار کمینهی هر یک از ستونها : نتیجه در یک بردار سطری داده میشود ans = ۷ ۷ ۱ ۳۳ ۸ >> max(A) ans = ۴۸ ۴۵ ۴۷ ۴۶ ۳۷ >> min(A')' از این تکنیک برای محاسبهی کمینهی سطرها استفاده میکنیم ans = ۷۷ ۲۱ ۱ >> max(A')' ans = ۴۲ ۴۸ ۴۷ ۴۵ >> [me ma]=min(A) با دو خروجی برای یک ماتریس min فراخوانی دستور me = ۷ ۷ ۱ ۳۳ ۸ ma = ۱ ۲ ۴ ۳ ۴ شماره سطری که مقدار بیشینه در آن واقع است >> [me ma]=max(A) me = ۴۸ ۴۵ ۴۷ ۴۶ ۳۷ ma = ۲ ۴ ۲ ۲ ۱ >> min(min(A)) مقدار کمینه یک ماتریس دو بعدی ans = ۱ >> max(max(A)) ans = ۴۸
چرخش ماتریس ها
آموزش رایگان متلب (fliplr(a: برای یک بردار آرایه ها را از آخر به اول می چیند و برای ماتریس ستون ها بدین ترتیب چیده می شوند
(flipud(A: برای یک ماتریس سطرها را از آخر به اول می چیند
(minmax(a: کمینه و بیشینه ی a بردار را بدست می دهد در صورتی که ورودی یک ماتریس باشد کمینه و بیشینه ی سطرها را بدست می دهد.
(rot90(A , k: این دستور ماتریس A را K*90 درجه در جهت مثبت مثلثاتی (پاد ساعتگرد) می چرخاند
>> a=[1 5 20 -5 -6 8 5 9 10 -8];
>> b=randint(1,10,20)
b =
۱۶ ۱۸ ۲ ۱۸ ۱۲ ۱ ۵ ۱۰ ۱۹ ۱۹
>> a=[1 5 20 -5 -6 8 5 9 10 -8]
a =
۱ ۵ ۲۰ -۵ -۶ ۸ ۵ ۹ ۱۰ -۸
>> c=fliplr(a) از آخر به اول a چیدن
c =
-۸ ۱۰ ۹ ۵ ۸ -۶ -۵ ۲۰ ۵ ۱
>> a(end:-1:1) fliplr کار معادل
ans =
-۸ ۱۰ ۹ ۵ ۸ -۶ -۵ ۲۰ ۵ ۱
>> A=randint(4,5,50)
A =
۳۵ ۴ ۴۷ ۳۸ ۲۲
۱ ۴۱ ۱ ۳۹ ۳۲
۱۳ ۳۴ ۲۱ ۹ ۳۵
۲ ۱۵ ۱۹ ۲۴ ۳۷
>> fliplr(A) چیدن ستونها از آخر به اول
ans =
۲۲ ۳۸ ۴۷ ۴ ۳۵
۳۲ ۳۹ ۱ ۴۱ ۱
۳۵ ۹ ۲۱ ۳۴ ۱۳
۳۷ ۲۴ ۱۹ ۱۵ ۲
>> A(:,end:-1:1) ماتریسی fliplr معادل
ans =
۲۲ ۳۸ ۴۷ ۴ ۳۵
۳۲ ۳۹ ۱ ۴۱ ۱
۳۵ ۹ ۲۱ ۳۴ ۱۳
۳۷ ۲۴ ۱۹ ۱۵ ۲
>> flipud(A) چیدن سطرها از آخر به اول
ans =
۲ ۱۵ ۱۹ ۲۴ ۳۷
۱۳ ۳۴ ۲۱ ۹ ۳۵
۱ ۴۱ ۱ ۳۹ ۳۲
۳۵ ۴ ۴۷ ۳۸ ۲۲
>> A(end:-1:1,:) ماتریسی flipud معادل
ans =
۲ ۱۵ ۱۹ ۲۴ ۳۷
۱۳ ۳۴ ۲۱ ۹ ۳۵
۱ ۴۱ ۱ ۳۹ ۳۲
۳۵ ۴ ۴۷ ۳۸ ۲۲
>> minmax(a)
ans =
-۸ ۲۰
>> A=magic(4)
A =
۱۶ ۲ ۳ ۱۳
۵ ۱۱ ۱۰ ۸
۹ ۷ ۶ ۱۲
۴ ۱۴ ۱۵ ۱
>> minmax(A)
ans =
۲ ۱۶
۵ ۱۱
۶ ۱۲
۱ ۱۵
------- rot --------- یک مثال خاص برای ۹۰
>> A=imread('cameraman.tif');
کار داریم rot فعلا دستور متلب را فقط به این صورت تایپ میکنیم و تنها با ۹۰
>> imshow(A) نتیجه را در متلب ببینید
>> B=rot90(A); چرخش ۹۰ درجهای یک تصویر
>> imshow(B) چرخش ۹۰ درجهای تصویر را در متلب ببینید
چند تابع ریاضی
(sign : sign(a تابع علامت است و برای مقادیر مثبت ۱ مقادیر منفی ۱- و برای صفر مقدار ۰ را برمی گرداند.
(abs : abs(a تابع قدر مطلق است البته کارکردی دیگر برای اعداد مختلط دارد که در زیرفصل مربوطه ذکر خواهد شد.
(sqrt : sqrt(a تابع رادیکال می باشد و می توان بجای آن بسادگی از و یا در ۰.۵^ a و یا در صورت برداری و یا ماتریسی بودن ورودی از A.^0.5 استفاده کرد.
>> sign(-15.2) ans = -۱ >> sign(0) ans = ۰ >> a=-4:4 a = -۴ -۳ -۲ -۱ ۰ ۱ ۲ ۳ ۴ >> sign(a) ans = -۱ -۱ -۱ -۱ ۰ ۱ ۱ ۱ ۱ >> abs(a) ans = ۴ ۳ ۲ ۱ ۰ ۱ ۲ ۳ ۴ >> b=2:8 b = ۲ ۳ ۴ ۵ ۶ ۷ ۸ >> sqrt(b) ans = ۱.۴۱۴۲ ۱.۷۳۲۱ ۲.۰۰۰۰ ۲.۲۳۶۱ ۲.۴۴۹۵ ۲.۶۴۵۸ ۲.۸۲۸۴ >> b.^0.5 ans = ۱.۴۱۴۲ ۱.۷۳۲۱ ۲.۰۰۰۰ ۲.۲۳۶۱ ۲.۴۴۹۵ ۲.۶۴۵۸ ۲.۸۲۸۴
(sum(a: این دستور بسیار پرکاربرد است و با توانایی استفاده از آن می توانیم بسیاری از حلقه های for را از برنامه حذف کنیم، سرعت اجرای برنامه را زیاد و برنامه را خواناتر کنیم.
>> sum(4,2) برای جمع دو عدد نیست sum دستور ans = ۴ >> a=-20:10:60 a = -۲۰ -۱۰ ۰ ۱۰ ۲۰ ۳۰ ۴۰ ۵۰ ۶۰ >> b=[4 -5 12 0 8 23 5 20 -12] b = ۴ -۵ ۱۲ ۰ ۸ ۲۳ ۵ ۲۰ -۱۲ >> sum(a) جمع همهی درایهها ans = ۱۸۰ >> sum(b) ans = ۵۵ >> sum(abs(a)) جمع قدر مطلق همهی درایهها ans = ۲۴۰ >> sum(abs(b)) ans = ۸۹ >> sum(a-b) ans = ۱۲۵ >> sum(abs(a-b)) ans = ۲۰۷ >> sum(a.^2) جمع توان دو همهی عناصر ans = ۹۶۰۰ >> sum((a-b).^2) ans = ۸۳۴۷ >> B=[1 2 3 4 5; 6 7 8 9 10; 11 12 13 14 15 ] B = ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ ۱۰ ۱۱ ۱۲ ۱۳ ۱۴ ۱۵ >> D=(B-5)*3 D = -۱۲ -۹ -۶ -۳ ۰ ۳ ۶ ۹ ۱۲ ۱۵ ۱۸ ۲۱ ۲۴ ۲۷ ۳۰ >> sum(B) جمع همهی ستونها ans = ۱۸ ۲۱ ۲۴ ۲۷ ۳۰ >> sum(B,1) ans = ۱۸ ۲۱ ۲۴ ۲۷ ۳۰ (... جمع همهی ستونها (عدد ۱ بعدی است که عمل جمع در آن صورت میگیرد بعد سطری ۱ بعد ستونی ۲ و >> sum(B,3) ans = ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ ۱۰ ۱۱ ۱۲ ۱۳ ۱۴ ۱۵ در بعد سوم (چون این ماتریس دو بعد بیشتر ندارد جمع روی بعد سوم خود ماتریس را نتیجه میدهد) B جمع عناصر >> sum(4,3) مشابه مورد بالا ans = ۴ >> sum(B,2) جمع همهی سطرها ans = ۱۵ ۴۰ ۶۵ >> sum(D,1) ans = ۹ ۱۸ ۲۷ ۳۶ ۴۵ >> sum(D,2) ans = -۳۰ ۴۵ ۱۲۰ >> sum(sum(B)) جمع همهی عناصر ans = ۱۲۰ >> sum(sum(D)) ۱۳۵ >> sum(sum(abs(D))) ans = ۱۹۵ >> sum(sum(abs(B-D))) ans = ۱۱۳
(prod(a: حاصلضرب درایه ها را حساب می کند و اگر ورودی ماتریس باشد نتیجه حاصلضرب ستون ها است.
>> a=2:6 a = ۲ ۳ ۴ ۵ ۶ >> prod(a) ans = ۷۲۰ >> A=magic(3) A = ۸ ۱ ۶ ۳ ۵ ۷ ۴ ۹ ۲ >> prod(A) حاصلضرب ستونها ans = ۹۶ ۴۵ ۸۴ >> prod(size(A)) استفاده میشود numel عموما از این عبارت بجای دستور ans = ۹ >> numel(A) ans = ۹
جمع و ضرب تجمعی
(cumsum(a: جمع تجمعی را حساب می کند و نتیجه یک بردار است این دستور در بیشتر در محاسبه ی توزیع تجمعی از روی توزیع احتمال کاربرد دارد.
(cumprod(a: عملکرد مشابه cumsum در حوزه ی ضرب
>> a=1:5 a = ۱ ۲ ۳ ۴ ۵ >> b=-4:3:8 b = -۴ -۱ ۲ ۵ ۸ >> cumsum(a) cumulative sum ans = ۱ ۳ ۶ ۱۰ ۱۵ >> cumsum(b) ans = -۴ -۵ -۳ ۲ ۱۰ >> cumprod(a) ans = ۱ ۲ ۶ ۲۴ ۱۲۰ >> cumprod(b) ans = -۴ ۴ ۸ ۴۰ ۳۲۰
توابعی از آمار ریاضی
(mean(a: میانگین بردار a را بدست می دهد. اگر ورودی یک ماتریس باشد نتیجه میانگین ستون ها است
(median(a: میانه ی a را نتیجه می دهد و بیشتر یک دستور آماری است
(var(a: واریانس یک بردار را بدست می دهد معادل عبارت ریاضی . اگر ورودی یک ماتریس باشد نتیجه واریانس ستون ها است.
(std(a: پراکندگی استاندارد آرایه ی ورودی را بدست می دهد که معادل عبارت ریاضی است اگر ورودی یک ماتریس باشد نتیجه پراکندگی استاندارد ستون ها است
>> a=[5 8 -3 25 12 -8 30 0 3] a = ۵ ۸ -۳ ۲۵ ۱۲ -۸ ۳۰ ۰ ۳ >> b=[15 -13 0 5 1 -5 10 10 3] b = ۱۵ -۱۳ ۰ ۵ ۱ -۵ ۱۰ ۱۰ ۳ >> mean(a) ans = ۸ >> mean(b) ans = ۲.۸۸۸۹ >> var(a) ans = ۱۵۸ >> std(a) ans = ۱۲.۵۶۹۸ >> std(a)^2 ans = ۱۵۸ >> I=(sum(a.^2-mean(a)^2))/(length(a)-1) I = ۱۵۸
(norm(a: نرم یک آرایه را حساب می کند که برای آرایه بصورت تعریف می شود در حالت کلی توان میتواند یک عدد دلخواه باشد که برای این منظور تابع نرم را با دو ورودی فراخوانی می کنیم (norm(a , p
>> a=10:5:40 a = ۱۰ ۱۵ ۲۰ ۲۵ ۳۰ ۳۵ ۴۰ >> norm(a) ans = ۷۱.۲۳۹۰ >> sqrt(sum(a.^2)) ans = ۷۱.۲۳۹۰ >> norm(a,10) ans = ۴۱.۱۵۵۶ >> (sum(a.^10))^0.1 ans = ۴۱.۱۵۵۶
مرتب کردن آرایه ها
(sort(a: این دستور آرایه را به ترتیب از مقدار کوچک به بزرگ می چیند
() find: این دستور برای جستجو و پیداکردن مقادیر خاص در آرایه ها و ماتریس ها بکار می رود و استفاده از آن پیش نیاز عبارتهای شرطی را می طلبد و در اینجا در حد آشنایی ساده مطرح می شود و بحث کامل تا کار با آرایه های شرطی به تعویق می افتد
>> a=[13 17 -15 17 5 -17 -9 2 19 19] a = ۱۳ ۱۷ -۱۵ ۱۷ ۵ -۱۷ -۹ ۲ ۱۹ ۱۹ >> a1=sort(a) a1 = -۱۷ -۱۵ -۹ ۲ ۵ ۱۳ ۱۷ ۱۷ ۱۹ ۱۹ >>[a1 ind]=sort(a) مرتب کردن صعودی علاوهی اندیس عناصر a1 = -۱۷ -۱۵ -۹ ۲ ۵ ۱۳ ۱۷ ۱۷ ۱۹ ۱۹ ind = ۶ ۳ ۷ ۸ ۵ ۱ ۲ ۴ ۹ ۱۰ >> sort(a,'ascend') صعودی ans = -۱۷ -۱۵ -۹ ۲ ۵ ۱۳ ۱۷ ۱۷ ۱۹ ۱۹ >> sort(a,'descend') نزولی ans = ۱۹ ۱۹ ۱۷ ۱۷ ۱۳ ۵ ۲ -۹ -۱۵ -۱۷ >> a1(end:-1:1) یک روش دیگر برای مرتبکردن نزولی ans = ۱۹ ۱۹ ۱۷ ۱۷ ۱۳ ۵ ۲ -۹ -۱۵ -۱۷ >> A=magic(4) A = ۱۶ ۲ ۳ ۱۳ ۵ ۱۱ ۱۰ ۸ ۹ ۷ ۶ ۱۲ ۴ ۱۴ ۱۵ ۱ >> sort(A) ans = ستونها بصورت نزولی مرتب شدهاند ۴ ۲ ۳ ۱ ۵ ۷ ۶ ۸ ۹ ۱۱ ۱۰ ۱۲ ۱۶ ۱۴ ۱۵ ۱۳ >> sort(A,1) ستون ها بصورت نزولی مرتب شود ans = ۴ ۲ ۳ ۱ ۵ ۷ ۶ ۸ ۹ ۱۱ ۱۰ ۱۲ ۱۶ ۱۴ ۱۵ ۱۳ >> sort(A,2) سطرها بترتیب نزولی مرتب شوند ans = ۲ ۳ ۱۳ ۱۶ ۵ ۸ ۱۰ ۱۱ ۶ ۷ ۹ ۱۲ ۱ ۴ ۱۴ ۱۵ >> ind=find(a==2) ind = برابر ۲ است a خروجی اندیس جایی است که در آن ۸ در اینجا از عبارت == استفاده میکنیم توضیح در عبارتهای شرطی خواهد آمد >> a(ind) ans = ۲ >> ind=find(a==17) ind = ۲ ۴ >> a(ind) ans = ۱۷ ۱۷
[av_hr class=’custom’ height=’50’ shadow=’no-shadow’ position=’center’ custom_border=’av-border-fat’ custom_width=’50px’ custom_border_color=” custom_margin_top=’30px’ custom_margin_bottom=’30px’ icon_select=’yes’ custom_icon_color=’#f6b93b’ icon=’ue80c’ font=’entypo-fontello’ av_uid=’av-384ph5′ custom_class=” admin_preview_bg=”]
کاربرد متلب در مهندسی صنایع(آموزش ویدیویی)
[av_image_hotspot src=’https://sanayesoft.com/blog/wp-content/uploads/2019/08/matlab_software_sanayesoft-495×400.jpg’ attachment=’5528′ attachment_size=’portfolio’ animation=’fade-in’ hotspot_layout=’numbered’ hotspot_tooltip_display=’av-permanent-tooltip’ av_uid=’av-3okwzj’ custom_class=”] [av_image_spot tooltip_pos=’av-tt-pos-above av-tt-align-left’ tooltip_width=’av-tt-default-width’ tooltip_style=’main_color’ link=’product,4337′ link_target=’_blank’ hotspot_color=” custom_bg=’#ffffff’ custom_font=’#888888′ custom_pulse=’#ffffff’ hotspot_pos=” av_uid=’av-2lgqjj’] کلیک کنید.
[/av_image_spot] [/av_image_hotspot]
امیدواریم از این مطلب در سایت صنایع سافت که درباره آموزش رایگان متلب بود، لذت برده باشید.نظرات خودتون رو واسه ما کامنت بزارین تا ما بتونیم هر چه بیشتر از اونها واسه بهتر شدنه تیممون استفاده کنیم.
[av_hr class=’custom’ height=’50’ shadow=’no-shadow’ position=’center’ custom_border=’av-border-fat’ custom_width=’50px’ custom_border_color=” custom_margin_top=’30px’ custom_margin_bottom=’30px’ icon_select=’yes’ custom_icon_color=’#f6b93b’ icon=’ue80c’ font=’entypo-fontello’ av_uid=’av-384ph5′ custom_class=” admin_preview_bg=”][av_notification title=” icon_select=’no’ icon=’ue800′ font=’entypo-fontello’ color=’custom’ border=” custom_bg=’#34495e’ custom_font=’#ffffff’ size=’large’ close_btn=” cookie_lifetime=’نامکاربری نمیتواند بیشتر از ۶۰ حرف باشد.’ av_uid=’av-2prgta’ admin_preview_bg=”]
حتما شما هم علاقه مندید مثله بقیه مهندسان صنایع از مقاله های جدید ما باخبر بشین، خب فقط کافیه ایمیلتونو داخل فرم زیر وارد کنید و دکمه ارسال رو بزنید. به همین راحتی 🙂
[/av_notification]
[av_testimonials style=’grid’ columns=’1′ grid_style=” interval=’5′ font_color=” custom_title=” custom_content=” av_uid=’av-4ly8tv’ admin_preview_bg=”] [av_testimonial_single src=’4200′ name=’احمد جعفری’ subtitle=” link=’http://’ linktext=” av_uid=’av-1vkktv’] کارشناسی رشته مهندسی صنایع، فعال در حوزه دیجیتال مارکتینگ و علاقه مند به استارت اپ ها
هدفم اینه که بازار کار رشته صنایع رو برای فعالین این حوزه شفاف تر کنم.
[/av_testimonial_single] [/av_testimonials] [av_hr class=’custom’ height=’50’ shadow=’no-shadow’ position=’center’ custom_border=’av-border-fat’ custom_width=’50px’ custom_border_color=” custom_margin_top=’30px’ custom_margin_bottom=’30px’ icon_select=’yes’ custom_icon_color=’#f6b93b’ icon=’ue80c’ font=’entypo-fontello’ av_uid=’av-384ph5′ custom_class=” admin_preview_bg=”]
اگر این مقاله برای شما مفید بود برای دوستان خود هم به اشتراک بگذارید تا بقیه هم از این مطلب استفاده لازم را ببرند.



