آموزش متلب برای مهندسی صنایع | (قسمت چهارم)
آموزش متلب برای مهندسی صنایع
آموزش متلب برای مهندسی صنایع در این قسمت از آموزش های نرم افزارهای مهندسی صنایع به قسمت بعدی از آموزش نرم افزار متلب برای مهندسان صنایع میپردازیم. فهرست این آموزش شامل موارد زیر است:
- توابع اعداد مختلط
- عبارتهای جبری
- جبر ماتریسی
- ضرب کرونکر
- دستگاه معادلات خطی
- تجزیه ی LU
- حل معادله چند مجهولی به روش LU
- عبارتهای جبری ماتریسی
- مقادیر ویژه و بردارهای ویژه

آموزش رایگان برای شما، کلیک کنید : آموزش رایگان متلب
توابع اعداد مختلط
(conj(a: مزدوج مختلط عدد را میدهد. بدین منظور می توان عملگر ‘ را برای عدد و عملگر ‘.’ را برای آرایه و یا ماتریس استفاده کرد
(real(a: قسمت حقیقی عدد مختلط
(imag(x: قسمت موهومی عدد مختلط
(abs(a: اندازه ی عدد مختلط
(angle(a: فاز عدد مختلط بر حسب رادیان
>> a=4-3i a = ۴.۰۰۰۰ - ۳.۰۰۰۰i >> b=5-8i b = ۵.۰۰۰۰ - ۸.۰۰۰۰i >> d=[1-3i 4-5i -2-5i 4-8i] d = ۱.۰۰۰۰ - ۳.۰۰۰۰i 4.0000 - 5.0000i -2.0000 - 5.0000i ۴.۰۰۰۰ - ۸.۰۰۰۰i >> a' ans = ۴.۰۰۰۰ + ۳.۰۰۰۰i >> conj(a) ans = ۴.۰۰۰۰ + ۳.۰۰۰۰i >> conj(d) ans = ۱.۰۰۰۰ + ۳.۰۰۰۰i 4.0000 + 5.0000i -2.0000 + 5.0000i ۴.۰۰۰۰ + ۸.۰۰۰۰i >> d'.' ans = ۱.۰۰۰۰ + ۳.۰۰۰۰i 4.0000 + 5.0000i -2.0000 + 5.0000i ۴.۰۰۰۰ + ۸.۰۰۰۰i >> real(a) ans = ۴ >> real(d) ans = ۱ ۴ -۲ ۴ >> imag(a) ans = -۳ >> imag(d) ans = -۳ -۵ -۵ -۸ >> abs(a) ans = ۵ >> abs(d) ans = ۳.۱۶۲۳ ۶.۴۰۳۱ ۵.۳۸۵۲ ۸.۹۴۴۳ >> angle(a) ans = -۰.۶۴۳۵ >> angle(d) ans = -۱.۲۴۹۰ -۰.۸۹۶۱ -۱.۹۵۱۳ -۱.۱۰۷۱ >> 180/pi*angle(d) زاویه بر حسب درجه ans = -۷۱.۵۶۵۱ -۵۱.۳۴۰۲ -۱۱۱.۸۰۱۴ -۶۳.۴۳۴۹
دستور ()sort برای اعداد مختلط اندازه ی عدد مختلط را معیار قرار می دهد و بر این اساس اعداد را بترتیب صعودی (در اندازه) مرتب می کند در صورت یکسان بودن اندازه عددی که فاز بزرگتری دارد بزرگ حساب می شود.
>> q=[-9 1+1i 8 3-5i 1-1i 3+5i 6] q = Columns 1 through 4 -۹.۰۰۰۰ ۱.۰۰۰۰ + ۱.۰۰۰۰i 8.0000 3.0000 - 5.0000i Columns 5 through 7 ۱.۰۰۰۰ -۱.۰۰۰۰i 3.0000 + 5.0000i 6.0000 >> w=sort(q) w = Columns 1 through 3 ۱.۰۰۰۰ - ۱.۰۰۰۰i 1.0000 + 1.0000i 3.0000 - 5.0000i Columns 4 through 7 ۳.۰۰۰۰ + ۵.۰۰۰۰i 6.0000 8.0000 -9.0000 >> abs(w) اندازه بترتیب صعودی است ans = ۱.۴۱۴۲ ۱.۴۱۴۲ ۵.۸۳۱۰ ۵.۸۳۱۰ ۶.۰۰۰۰ ۸.۰۰۰۰ ۹.۰۰۰۰ >> angle(w) ans = -۰.۷۸۵۴ ۰.۷۸۵۴ -۱.۰۳۰۴ ۱.۰۳۰۴ ۰ ۰ ۳.۱۴۱۶
عبارتهای جبری
در ادامه آموزش متلب برای مهندسی صنایع در این قسمت پس از یادگیری و آشنایی با توابع مختلف می خواهیم صورت متلبی عبارتهای جبری را که عموما به آنها برخورد می کنیم را بنویسیم. برای آشنایی بیشتر مثالهای زیر را دنبال کنید
فرض کنید x در حالت کلی یک آرایه ی برداری بصورت باشد [x=[x1 x2 …xN
صورت متلبی عبارتهای جبری زیر را بنویسید (جواب در سمت راست نوشته شده است)
sin ( ) >> sin(x) cos ( ) >> cos(x) sin ( ) >> asin(x) sinh ( ) >> sinh(x) sinh ( ) >> asinh(x) tgh ( ) >> atanh(x) e >> exp(x) log ( ) >> log10(x) Ln( ) >> log(x) ( ) ∗ () >> ().*() ⟾ حالت کلی e >> sin(x)./x x sin ( ) >> exp(-x.^2) x sin ( ) >> x.*sin(x) >> x.*sin(x.^2) sin ( ) >> ()./() ⟾ حالت کلی x >> (x.^3-3*x+4)./(x.^2-13) − ۳ + ۴ x − ۱۳ >> ((x.^2).*sin(x) – cos(x)) ... x sin( ) − cos ( ) ./(x.^3 – ۳*x) x − ۳x x e >> x.*exp(-(x.^2)./(x+3) ) x − >> x – x./( x.^2 - 1 ) − ۱ >> x– x/( x.^2 - 1 )⟾ ایراد دستوری ندارد ولی صحیح نیست e − x >> exp(x)-x.^2 >> ( exp(x)- x.^2 )./( exp(x)+exp(-x) ) e − x e + e >> ( exp(x)- x.^2 )./( exp(x)+exp(-x) ) e − x e + e
اگر a و b دو بردار با طول یکسان باشند a./b تقسیم آشنای عنصر به عنصر است نکته ی قابل توجه این است که a/b نیز در متلب تعریف شده است (‘a/b = a*b’/(b*b و در صورتیکه از عملگر / بجای /. استفاده کنیم ایراد نگارشی وجود ندارد ولی عبارت محاسبه شده با عبارت مورد نظر ما متفاوت است لذا لازم است در نوشتن عبارت تقسیم عنصر به عنصر دو بردار دقت کافی داشته باشیم
- یادآوری چند نکته در مورد صفحه فرمان (command window)
در اینجا چند نکته برای آشنایی اولیه با صفحه فرمان ذکر می کنیم.
- ابتدای دستور متلب علامت << قرار دارد
- اگر در ابتدای خط فرمان جاری کلید بالاپیمای ↑ صفحه کلید را فشار دهیم به دستور قبل می رسیم
- اگر عبارتی را تایپ و سپس کلید بالاپیما ↑ را فشار دهیم دستور قبلی متلب که با این عبارت آغاز می شود در خط فرمان جاری ظاهر خواهد شد مثال a=↑ و یا sort↑ (علامت ↑ در اینجا بمعنای فشردن کلید بالاپیما است)
- کلیدEsc خط فرمان جاری را پاک می کند
- دستور clcموجب پاک شدن صفحه فرمان می شود
- پاک شدن صفحه بمعنای پاک شدن متغیرها نیست
جبر ماتریسی
در این قسمت ما با عملیات مختلف ماتریسی در متلب آشنا می شویم
A*B: ضرب ماتریسی دو ماتریس A و B
‘.A: ترانهاده A
(det(A: دترمینان A
(inv(A: معکوس A
(diag(A: قطر اصلی A
>> A=magic(3) A = ۸ ۱ ۶ ۳ ۵ ۷ ۴ ۹ ۲ >> A.' ans = ۸ ۳ ۴ ۱ ۵ ۹ ۶ ۷ ۲ >> diag(A) ans = ۸۵۲ >> diag(diag(A)) ans = ۸ ۰ ۰ ۰ ۵ ۰ ۰ ۰ ۲ >> det(A) |A| ans = -۳۶۰ >> det(A)*det(inv(A)) |A | = 1/|A | ans = ۱ >> inv(A) ans = ۰.۱۴۷۲ -۰.۱۴۴۴ ۰.۰۶۳۹ -۰.۰۶۱۱ ۰.۰۲۲۲ ۰.۱۰۵۶ -۰.۰۱۹۴ ۰.۱۸۸۹ -۰.۱۰۲۸ >> A^-1 را نتیجه میدهد A همان معکوس ans = ۰.۱۴۷۲ -۰.۱۴۴۴ ۰.۰۶۳۹ -۰.۰۶۱۱ ۰.۰۲۲۲ ۰.۱۰۵۶ -۰.۰۱۹۴ ۰.۱۸۸۹ -۰.۱۰۲۸ >> inv(A)*A ans = ۱.۰۰۰۰ ۰ -۰.۰۰۰۰ ۰ ۱.۰۰۰۰ ۰ ۰ ۰.۰۰۰۰ ۱.۰۰۰۰
>> B=(A-4) B = ۴ -۳ ۲ -۱ ۱ ۳ ۰ ۵ -۲ >> B/A B/A ≡ B*A ans = ۰.۷۳۳۳ -۰.۲۶۶۷ -۰.۲۶۶۷ -۰.۲۶۶۷ ۰.۷۳۳۳ -۰.۲۶۶۷ -۰.۲۶۶۷ -۰.۲۶۶۷ ۰.۷۳۳۳ >> B*inv(A) ans = ۰.۷۳۳۳ -۰.۲۶۶۷ -۰.۲۶۶۷ -۰.۲۶۶۷ ۰.۷۳۳۳ -۰.۲۶۶۷ -۰.۲۶۶۷ -۰.۲۶۶۷ ۰.۷۳۳۳
ضرب کرونکر
(kron(A,B: ضرب کرونکر B,A
در ادامه آموزش متلب برای مهندسی صنایع ضرب کرونکر را می توانیم بدین صورت بیان کنیم که در آن هر درایه ی ماتریس A در همه ی ماتریس B ضرب می شود. و توجه داریم که با توجه به تعریف این ضرب قابلیت جابجایی ندارد. در بعضی از مباحث پیشرفته استفاده از این دستور میتواند بر سرعت و خوانایی برنامه بیافزاید. برای مثال A یک ماتریس ۳×۲ باشد ضرب کرونکر B,A بصورت زیر است.
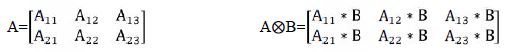
که B یک ماتریس است
(kron(ones(n,m),A ماتریس A را در n سطر m ستون تکرار می کند و معادل دستور (repmat(A,n,m است
>> A=[1 1;1 1] A = ۱ ۱ ۱ ۱ >> B=[2 3] B = ۲ ۳ >> kron(A,B) ans = ۲ ۳ ۲ ۳ ۲ ۳ ۲ ۳ >> kron(B,A) kron(A,B) ≠ kron(B,A) ans = ۲ ۲ ۳ ۳ ۲ ۲ ۳ ۳ >> C=[1 2;3 4] C = ۱ ۲ ۳ ۴ >> kron(A,C) ans = ۱ ۲ ۱ ۲ ۳ ۴ ۳ ۴ ۱ ۲ ۱ ۲ ۳ ۴ ۳ ۴ >> s=[1 5 8 -2 4] s = ۱ ۵ ۸ -۲ ۴ >> kron(ones(1,3),s) ans = ۱ ۵ ۸ -۲ ۴ ۱ ۵ ۸ -۲ ۴ ۱ ۵ ۸ -۲ ۴ از این تکنیک برای تکرار به تعداد دلخواه یک آرایه استفاده میشود >> kron(s,ones(1,3)) از این تکنیک برای چندین تکرار یک عنصر استفاده میشود ans = ۱ ۱ ۱ ۵ ۵ ۵ ۸ ۸ ۸ -۲ -۲ -۲ ۴ ۴ ۴
(rank(A: رنک یک ماتریس تعداد سطرها و یا ستونهایی که از یکدیگر مستقل خطی هستند
>> A=[1 0;0 1] A = ۱ ۰ ۰ ۱ >> B=[1 2;4 8] B = ۱ ۲ ۴ ۸ >> rank(A) ans = ۲ >> rank(B) ans = ۱
دستگاه معادلات خطی
در ادامه آموزش متلب برای مهندسی صنایع از ریاضیات مقدماتی می دانیم که یک دستگاه معادلات خطی را می توانیم بشکل ماتریسی بنویسیم
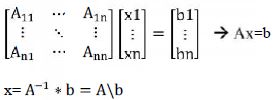
>> A=[4 3 -6;4 -2 3;2 4 7] A = ۴ ۳ -۶ ۴ -۲ ۳ ۲ ۴ ۷ >> b=[0; 2; -8] b = ۰۲ -۸ >> det(A) |A|≠۰ ans = -۲۹۰ >> x=inv(A)*b جواب معادله x = ۰.۲۲۷۶ -۱.۲۶۹۰ -۰.۴۸۲۸ >> x=A\b این فرم نوشتار سادهتر است و خود متلب نیز از آن استفاده میکند x = ۰.۲۲۷۶ -۱.۲۶۹۰ -۰.۴۸۲۸
تجزیه ی LU
در ادامه آموزش متلب برای مهندسی صنایع تجزیه ی LU یکی از روشهای قوی برای محاسبه ی معکوس ماتریس و حل معادله ی چند مجهولی ساده است که در آن، ماتریس را به دو ماتریس بالا مثلثی و پایین مثلثی تجزیه می کنیم که حاصلضرب آنها برابر ماتریس اصلی است چنین تفکیکی همیشه امکان پذیر نیست و شرایط خاصی را می طلبد یک راه حل برای اینکه به این روش مقداری عمومیت دهیم این است که سطرهای ماتریس اصلی را جابجا کرده سپس تجزیه ی LU را انجام دهیم .
(L1 [L1,U] = lu(A یک ماتریس پایین مثلثی است که سطرهای آن جابجا شده اند L1*U = A
(L,U,P] = lu(A] تجزیه به ماتریس های پایین مثلثی و بالا مثلثی در حالت کلی برای این کار باید سطرهای A جابجا شوند ماتریس P این کار را انجام می دهد LU = PA
(‘p [L,U,p] = lu(A,’vector را بصورت برداری ذخیره میکند که در کار با ماتریس های با ابعاد بالا از ذخیرهی داده و سرعت انجام برنامه میتواند بسیار مفید باشد
(triu(A: ماتریس A با عناصر مثلث بالا
(tril (A: ماتریس A با عناصر مثلث پایین
>> A = [1 2 3;4 5 6;7 8 0]; >> [L1,U] = lu(A) سطر ۲ و ۳ مربوط به ماتریس پایین مثلثی جابجا شدهاند L1 = ۰.۱۴۲۹ ۱.۰۰۰۰ ۰ ۰.۵۷۱۴ ۰.۵۰۰۰ ۱.۰۰۰۰ ۱.۰۰۰۰ ۰ ۰ U = ۷.۰۰۰۰ ۸.۰۰۰۰ ۰ ۰ ۰.۸۵۷۱ ۳.۰۰۰۰ ۰ ۰ ۴.۵۰۰۰ >> L1*U ans = ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۰ >> X = inv(U)*inv(L1) X = -۱.۷۷۷۸ ۰.۸۸۸۹ -۰.۱۱۱۱ ۱.۵۵۵۶ -۰.۷۷۷۸ ۰.۲۲۲۲ -۰.۱۱۱۱ ۰.۲۲۲۲ -۰.۱۱۱۱ >> [L2,U,P] = lu(A) L2 = ۱.۰۰۰۰ ۰ ۰ ۰.۱۴۲۹ ۱.۰۰۰۰ ۰ ۰.۵۷۱۴ ۰.۵۰۰۰ ۱.۰۰۰۰ U = ۷.۰۰۰۰ ۸.۰۰۰۰ ۰ ۰ ۰.۸۵۷۱ ۳.۰۰۰۰ ۰ ۰ ۴.۵۰۰۰ P = ۰ ۰ ۱ ۱ ۰ ۰ ۰ ۱ ۰ >> P*L1 ans = ۱.۰۰۰۰ ۰ ۰ ۰.۱۴۲۹ ۱.۰۰۰۰ ۰ ۰.۵۷۱۴ ۰.۵۰۰۰ ۱.۰۰۰۰ >> P*A - L2*U PA = L2U ans = ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ ۰ >> A=magic(3) A = ۸ ۱ ۶ ۳ ۵ ۷ ۴ ۹ ۲ >> tril(A) lower triangular ans = ۸ ۰ ۰ ۳ ۵ ۰ ۴ ۹ ۲ >> triu(A) upper triangular ans = ۸ ۱ ۶ ۰ ۵ ۷ ۰ ۰ ۲
حل معادله چند مجهولی به روش LU
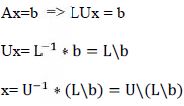
>> A=[4 3 -6;4 -2 3;2 4 7] A = ۴ ۳ -۶ ۴ -۲ ۳ ۲ ۴ ۷ >> b=[0; 2; -8] b = ۰۲ -۸ >> [L,U]=lu(A) L = ۱.۰۰۰۰ ۰ ۰ ۱.۰۰۰۰ ۱.۰۰۰۰ ۰ ۰.۵۰۰۰ -۰.۵۰۰۰ ۱.۰۰۰۰ U = ۴.۰۰۰۰ ۳.۰۰۰۰ -۶.۰۰۰۰ ۰ -۵.۰۰۰۰ ۹.۰۰۰۰ ۰ ۰ ۱۴.۵۰۰۰ >> x1=A^-1*b x1 = ۰.۲۲۷۶ -۱.۲۶۹۰ -۰.۴۸۲۸ >> x=U\(L\b) x = ۰.۲۲۷۶ -۱.۲۶۹۰ -۰.۴۸۲۸ >> A=magic(3) A = ۸ ۱ ۶ ۳ ۵ ۷ ۴ ۹ ۲ >> b=[3; 2; 8] b = ۳۲۸ >> [L,U,p] = lu(A,'vector') L = ۱.۰۰۰۰ ۰ ۰ ۰.۵۰۰۰ ۱.۰۰۰۰ ۰ ۰.۳۷۵۰ ۰.۵۴۴۱ ۱.۰۰۰۰ U = ۸.۰۰۰۰ ۱.۰۰۰۰ ۶.۰۰۰۰ ۰ ۸.۵۰۰۰ -۱.۰۰۰۰ ۰ ۰ ۵.۲۹۴۱ p = ۱ ۳ ۲ >> x1=A^-1*b x1 = ۰.۶۶۳۹ ۰.۷۰۵۶ -۰.۵۰۲۸ >> x=U\(L\(b(p))) x = ۰.۶۶۳۹ ۰.۷۰۵۶ -۰.۵۰۲۸
حل معادلات خطی بروش LU حدود ۲.۵ برابر از روش ماتریس سریعتر است (سرعت اجرای دستورها را می توان با روش های مختلف در متلب بدست آورد.
عبارتهای جبری ماتریسی
در ادامه آموزش متلب برای مهندسی صنایع در حل معادلهای مثل dx/dt =ax نتیجه بسادگی بدست می آید در حالت کلی تر اگر x یک بردار و A یک ماتریس باشد نتیجه ی مشابهی داریم:
![]()
برای محاسباتی از این دست به توابع ماتریسی برمی خوریم
(sqrtm(A: در A√ رادیکال ماتریسی یعنی عکس A*A در نتیجه خواهیم داشت
(expm(A
(ln(A) logm(A
>> A=magic(3) A = ۸ ۱ ۶ ۳ ۵ ۷ ۴ ۹ ۲ >> B=sqrtm(A) B = ۲.۷۰۶۵ + ۰.۰۶۰۱i 0.0185 + 0.5347i 1.1480 - 0.5948i ۰.۴۷۰۳ + ۰.۰۸۲۹i 2.0288 + 0.7378i 1.3739 - 0.8207i ۰.۶۹۶۲ - ۰.۱۴۳۰i 1.8257 - 1.2725i 1.3511 + 1.4155i >> D=B*B D = ۸.۰۰۰۰ + ۰.۰۰۰۰i 1.0000 + 0.0000i 6.0000 - 0.0000i ۳.۰۰۰۰ + ۰.۰۰۰۰i 5.0000 7.0000 + 0.0000i ۴.۰۰۰۰ - ۰.۰۰۰۰i 9.0000 - 0.0000i 2.0000 - 0.0000i >> B=expm(A) B = ۱.0e+006 * ۱.۰۸۹۸ ۱.۰۸۹۶ ۱.۰۸۹۷ ۱.۰۸۹۶ ۱.۰۸۹۷ ۱.۰۸۹۷ ۱.۰۸۹۶ ۱.۰۸۹۷ ۱.۰۸۹۷ >> B1=exp(A) B1 = ۱.0e+003 * ۲.۹۸۱۰ ۰.۰۰۲۷ ۰.۴۰۳۴ ۰.۰۲۰۱ ۰.۱۴۸۴ ۱.۰۹۶۶ ۰.۰۵۴۶ ۸.۱۰۳۱ ۰.۰۰۷۴ >> A=[0 -6 -1;6 2 -16;-5 20 -10]; >> x0=[1;1;1]; >> t=2; >> expm(t*A)*x0 ans = ۰.۰۰۳۵ -۰.۰۰۰۹ -۰.۰۰۳۵ >> D=logm(B) D = ۸.۰۰۰۰ ۱.۰۰۰۰ ۶.۰۰۰۰ ۳.۰۰۰۰ ۵.۰۰۰۰ ۷.۰۰۰۰ ۴.۰ ۹.۰۰۰۰ ۲.۰۰۰۰
مقادیر ویژه و بردارهای ویژه
در ادامه آموزش متلب برای مهندسی صنایع برای ماتریسی مثل A حل معادله ی ۰= |A-SI| منتج به حل معادله مشخصه ماتریس می شود که با حل معادله مشخصه مقادیر ویژه و از آنجا بردارهای ویژه بدست می آیند
(p = poly(A: نمایش برداری چند جمله ای مشخصه ماتریس A
از (tf(p,1 می توانیم برای نمایش معمولی چندجمله ای برداری p استفاده کنیم این دستور فعلا برای ما تنها ارزش نمایشی دارد
برای فرم نماشی معمولی میتوانیم از دستور (poly2sym(p نیز بهره بگیریم ولی این دستور جز در حالتی که ضرایب صحیح باشند جواب چندان روشنی نمی دهد و استفاده از آن به مشروط به آشنایی با محاسبات سمبلیک است.
در خصوص نمایش برداری چندجمله ای در مبحث چندجمله ای ها بطور مبسوط بحث خواهد شد
(V,D] = eigs(A]: مقادیر ویژه و بردارهای ویژه ی A، ماتریس D یک ماتریس قطری است که عناصر قطر اصلی آن مقادیر ویژه ماتریس و ماتریس V نیز ماتریسی است که ستون های آن بردارهای ویژه ی ماتریس A می باشند
>> A=[1 2 3;4 5 6;7 8 9]; >> p=poly(A) ( نمایش برداری چند جملهای ضرایب از توان بزرگتر به توان کوچک (توان صفر p = ۱.۰۰۰۰ -۱۵.۰۰۰۰ -۱۸.۰۰۰۰ -۰.۰۰۰۰ >> tf(p,1) Transfer function: s^3 - 15 s^2 - 18 s - 2.347e-014 یکی از دستورهای پایهای متلب در کنترل میباشد در اینجا از آن برای نمایش چند جملهای استفاده میکنیم tf() >> d=eig(A) d = ۱۶.۱۱۶۸ -۱.۱۱۶۸ -۰.۰۰۰۰ >> [V,D] = eig(A) V = -۰.۲۳۲۰ -۰.۷۸۵۸ ۰.۴۰۸۲ -۰.۵۲۵۳ -۰.۰۸۶۸ -۰.۸۱۶۵ -۰.۸۱۸۷ ۰.۶۱۲۳ ۰.۴۰۸۲ D = ۱۶.۱۱۶۸ ۰ ۰ ۰ -۱.۱۱۶۸ ۰ ۰ ۰ -۰.۰۰۰۰ >> d1=diag(D) d1 = ۱۶.۱۱۶۸ -۱.۱۱۶۸ -۰.۰۰۰۰ *>> G=inv(V)*A*V را به فضای با پایههای بردارهای ویژه منتقل میکند A تبدیل تشابهی : ماتریس G = ۱۶.۱۱۶۸ ۰.۰۰۰۰ ۰.۰۰۰۰ -۰.۰۰۰۰ -۱.۱۱۶۸ ۰.۰۰۰۰ ۰.۰۰۰۰ ۰.۰۰۰۰ ۰.۰۰۰۰ *>> sum(sum(abs(G-D))) G=D ans = ۱.۴۷۸۰e-014
[av_hr class=’custom’ height=’50’ shadow=’no-shadow’ position=’center’ custom_border=’av-border-fat’ custom_width=’50px’ custom_border_color=” custom_margin_top=’30px’ custom_margin_bottom=’30px’ icon_select=’yes’ custom_icon_color=’#f6b93b’ icon=’ue80c’ font=’entypo-fontello’ av_uid=’av-384ph5′ custom_class=” admin_preview_bg=”]
کاربرد متلب در مهندسی صنایع(آموزش ویدیویی)
[av_image_hotspot src=’https://sanayesoft.com/blog/wp-content/uploads/2019/08/matlab_software_sanayesoft-495×400.jpg’ attachment=’5528′ attachment_size=’portfolio’ animation=’fade-in’ hotspot_layout=’numbered’ hotspot_tooltip_display=’av-permanent-tooltip’ av_uid=’av-3okwzj’ custom_class=”] [av_image_spot tooltip_pos=’av-tt-pos-above av-tt-align-left’ tooltip_width=’av-tt-default-width’ tooltip_style=’main_color’ link=’product,4337′ link_target=’_blank’ hotspot_color=” custom_bg=’#ffffff’ custom_font=’#888888′ custom_pulse=’#ffffff’ hotspot_pos=” av_uid=’av-2lgqjj’] کلیک کنید.
[/av_image_spot] [/av_image_hotspot]
امیدواریم از این مطلب در سایت صنایع سافت که درباره آموزش متلب برای مهندسی صنایع بود، لذت برده باشید.نظرات خودتون رو واسه ما کامنت بزارین تا ما بتونیم هر چه بیشتر از اونها واسه بهتر شدنه تیممون استفاده کنیم.
[av_hr class=’custom’ height=’50’ shadow=’no-shadow’ position=’center’ custom_border=’av-border-fat’ custom_width=’50px’ custom_border_color=” custom_margin_top=’30px’ custom_margin_bottom=’30px’ icon_select=’yes’ custom_icon_color=’#f6b93b’ icon=’ue80c’ font=’entypo-fontello’ av_uid=’av-384ph5′ custom_class=” admin_preview_bg=”][av_notification title=” icon_select=’no’ icon=’ue800′ font=’entypo-fontello’ color=’custom’ border=” custom_bg=’#34495e’ custom_font=’#ffffff’ size=’large’ close_btn=” cookie_lifetime=’نامکاربری نمیتواند بیشتر از ۶۰ حرف باشد.’ av_uid=’av-2prgta’ admin_preview_bg=”]
حتما شما هم علاقه مندید مثله بقیه مهندسان صنایع از مقاله های جدید ما باخبر بشین، خب فقط کافیه ایمیلتونو داخل فرم زیر وارد کنید و دکمه ارسال رو بزنید. به همین راحتی 🙂
[/av_notification]
[av_testimonials style=’grid’ columns=’1′ grid_style=” interval=’5′ font_color=” custom_title=” custom_content=” av_uid=’av-4ly8tv’ admin_preview_bg=”] [av_testimonial_single src=’4200′ name=’احمد جعفری’ subtitle=” link=’http://’ linktext=” av_uid=’av-1vkktv’] کارشناسی رشته مهندسی صنایع، فعال در حوزه دیجیتال مارکتینگ و علاقه مند به استارت اپ ها
هدفم اینه که بازار کار رشته صنایع رو برای فعالین این حوزه شفاف تر کنم.
[/av_testimonial_single] [/av_testimonials] [av_hr class=’custom’ height=’50’ shadow=’no-shadow’ position=’center’ custom_border=’av-border-fat’ custom_width=’50px’ custom_border_color=” custom_margin_top=’30px’ custom_margin_bottom=’30px’ icon_select=’yes’ custom_icon_color=’#f6b93b’ icon=’ue80c’ font=’entypo-fontello’ av_uid=’av-384ph5′ custom_class=” admin_preview_bg=”]
اگر این مقاله برای شما مفید بود برای دوستان خود هم به اشتراک بگذارید تا بقیه هم از این مطلب استفاده لازم را ببرند.



