آموزش مینی تب (Minitab) | آزمون کولموگروف – اسمیرنف[تصویری]

آموزش مینی تب

آموزش مینی تب در آموزش های قبلی در رابطه با آموزش آزمون اندرسون دارلینگ در نرم افزار مینی تب (Minitab) صحبت کردیم در این مطلب به ادامه آموزش نرم افزار آماری مینی تب میپردازیم. این آموزش شامل موارد زیر است :

1. انجام آزمون کولموگروف – اسمیرنف با Minitab
2. نمودار تقارن (Symmetry plot)
3. طریقه رسم نمودار تقارن (Symmetry plot) با Minitab
4. روش های تبدیل مشخصه های کیفی غیر نرمال به نرمال

انجام آزمون کولموگروف – اسمیرنف با Minitab

مثال: میخواهیم داده های مثال قبل را که با آزمون اندرسون دارلینگ انجام دادیم این بار با آزمون کولموگروف-اسمیرنف انجام دهیم.

مسیر زیر را دنبال کنید:

در قسمت variable ستون  supp1 را وارد کنید و در قسمت  Tests For Normality آزمون Kolmogorov-Smirnov را انتخاب کنید.

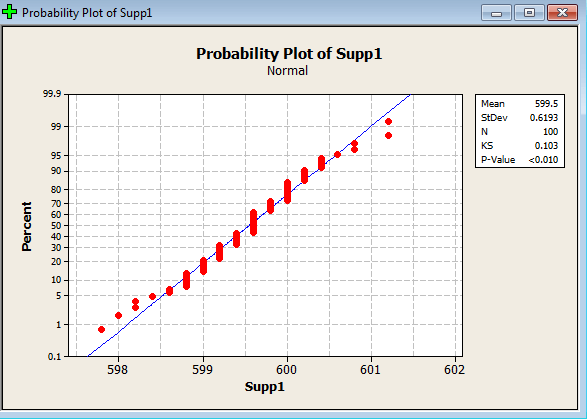
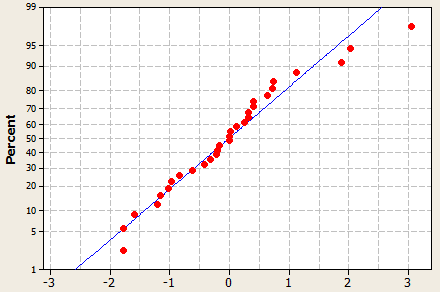
تحلیل: همانطور که در تصویر بالا پیداست مقدارP-Value  برای این آزمون کوچکتر از ۰.۰۵ شده پس فرض صفر مبنی بر اینکه مشاهداتمان توزیع نرمال دارند رد میشود. همچنین مشاهداتمان طرح احتمال نرمال را به خوبی پوشش ندادند.

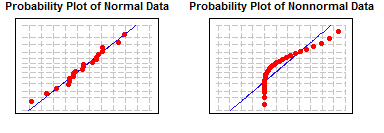
در صورتیکه داده های تصادفی بتوانند طرح احتمال نرمال را پوشش دهند پس میتوان گفت که مشاهداتمان توزیع نرمال دارند در غیر این صورت مشاهداتمان توزیع غیر نرمال دارند.

مطلب مرتبط : آموزش گام به گام نرم افزار مینی تب (Minitab) | [تصویری]

نمودار تقارن (Symmetry plot)

در ادامه آموزش مینی تب از این نموار برای بررسی و ارزیابی اینکه آیا داده های تصادفی از توزیع متقارن و نرمال پیروی می کنند یا نه، استفاده میشود. پس نمودار تقارن یکی دیگر از ابزارها برای بررسی نرمال بودن داده هایمان میباشد.

نمودار تقارن حالت خاصی از نمودار Probability Plot میباشد که فقط طرح احتمال نرمال را رسم میکند. نمودار تقارن یا نمودار احتمال را میتوان به عنوان جایگزینی برای نمودار هیستوگرام در جهت تعیین نوع تابع توزیع، مرکز و تغییر پذیری توزیع مشاهداتمان استفاده کرد.

نمودار احتمال نسبت به هیستوگرام از این برتری برخوردار است که دیگر ضرورتی برای تقسیم دامنه ی تغییرات به فواصل مختلف وجود ندارد. از طرف دیگر نمودار احتمال برای اندازه نمونه های نسبتا کوچک نتایج قابل قبولی را ارائه میکند (معمولا چنین نتایجی در هیستوگرام به دست نمی آید هم چنین در رسم هیستوگرام چون از تقسیم دامنه تغییرات بر تعداد  binها استفاده میکنیم باید از اندازه نمونه ی بزرگ استفاده کنیم تا به نتایج دقیق تری دست پیدا کنیم.)

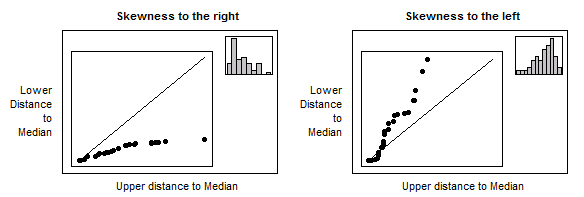
نمونه ای از یک نمودار تقارن است که بیانگر پیروی کردن متغیر تصادفی از توزیع نرمال میباشد. هرچقدر این نقاط به نمودار نزدیکتر باشند، تقارن بیشتری در داده ها وجود دارد. هرچند با داده های نرمال شده نیز، میتوانید انتظار وجود نقاطی در بالا یا پایین خط را داشته باشید.

دور شدن نقاط از خط اصلی در نمودار باعث ایجاد کجی در نمودار نرمال می شود و باعث می شود که این نمودار به سمت چپ یا راست گرایش پیدا کند. در صورتیکه مشاهداتمان به سمت بالای خط تقارن میل کنند یعنی مشاهداتمان چولگی به چپ دارند و اگر داده هایمان به سمت پایین خط میل کنند یعنی چولگی به راست در مشاهداتمان دیده میشود.

روش ایجاد یک طرح احتمال نرمال به این صورت است که ابتدا داده ها را به ترتیب صعودی مرتب میکنیم و آن ها را رتبه بندی میکنیم که نمونه ی اول دارای رتبه ۱ و نمونه ی آخر دارای رتبه n میباشد. سپس مکان رسم هر مشاهده دارای رتبه  j را دست می آوریم.

انحراف معیار مشاهدات نیز میتواند شیب خط مستقیم باشد. که در صورتیکه انحراف معیار واقعی جامعه را نداشته باشیم از انحراف معیار نمونه استفاده میکنیم.

در رسم طرح احتمال دو محور عمودی داریم که یکی برابر ۱۰۰ (۱-Pj)  و دیگری ۱۰۰ Pj با میباشد و محور افقی مربوط به مشاهدات میباشد.

آموزش رایگان  برای شما : کنترل فرایند اماری (SPC) در مینی تب

طریقه رسم نمودار تقارن (Symmetry plot) با Minitab

در ادامه آموزش مینی تب به بررسی یک مثال میپردازیم.
مثال: میخواهیم با توجه به مثال قبل نمودار تقارن را برای  supp1رسم کنیم. حال مراحل زیر را بری رسم نمودار انجام دهید:

• قدم ۱: از منوی File گزینه Open worksheet فایل Camshaft.mtw را انتخاب کنید.
• قدم ۲: مسیر زیر را دنبال کنید.

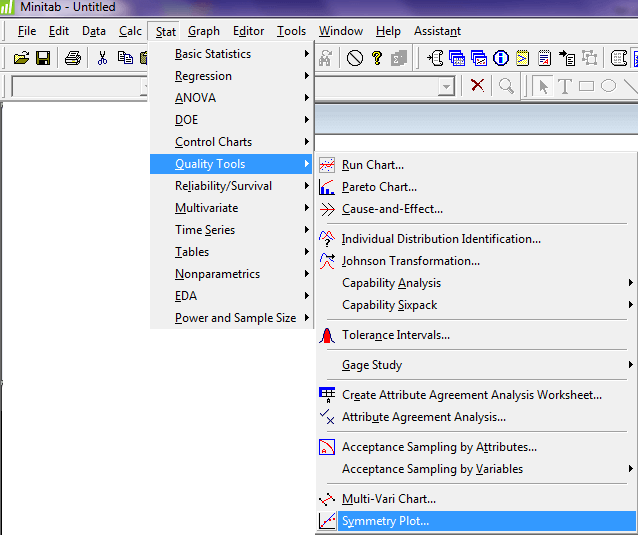
قدم ۳: در قسمت Variables سلول supp1 را وارد کنید و Ok را بزنید.

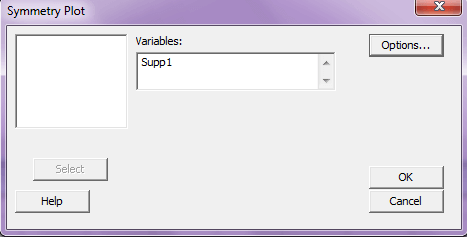
نتیجه ی کار به صورت نمودار زیر حاصل می شود:

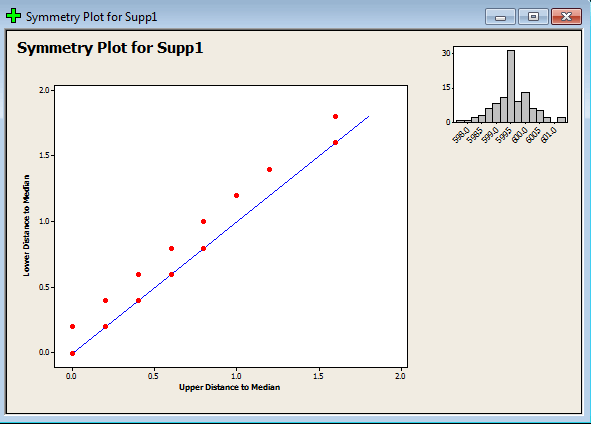
تحلیل: همانطور که از نمودار پیداست، تعداد نقاط کمی روی خط تقارن قرار گرفته اند. این نمودار نشان می دهند که خمیدگی در سمت چپ تابع توزیع است. به هیستوگرام نرمال توجه کنید.

حتما تا به حال از خود پرسیدید اگر مشاهدات ما توزیع نرمال نداشت باید چه کار کنیم؟ بسیاری از تحلیل گران ترجیح میدهند که اگر توزیع مشخصه کیفی تفاوت قابل ملاحظه ای با توزیع نرمال نداشته باشد، از روش های استاندارد مبتنی بر توزیع نرمال پیروی کنند.

محققان مختلفی اثر فاصله گرفتن از فرض توزیع نرمال را بر نمودارهای کنترل بررسی نمودند. تحقیقات به این نکته اشاره میکند که اثر فاصله گرفتن از توزیع نرمال بر روی ضرایب ثابت نمودار کنترل ناچیز است مگر اینکه جامعه ی مورد مطالعه با توزیع نرمال بیش از حد فاصله داشته باشد و یا به عبارت دیگر خیلی غیر نرمال باشد.

هم چنین این تحقیقات نیز اطلاعاتی در مورد اثر غیر نرمال بودن توزیع مشخصه ی کیفی بر حدود کنترل نمودار ارائه میکند در این اطلاعات، بررسی بر روی توزیع های یکنواخت، نرمال چولگی به راست، گاما با پارامتر مقیاس ۱ و پارامترهای شکل برابر ۱.۲,۱,۲,۳,۴ و یک توزیع ترکیبی دو نمایی که از ترکیب دو توزیع نرمال حاصل میگردد انجام گرفته است.

نتایج حاصل حاکی از این است که در اغلب موارد اندازه نمونه های ۴  یا ۵ تایی و تعداد نمونه گیری بالا (مثلا ۲۵ الی ۳۰) به اندازه کافی بزرگ هستند که با استفاده از قضیه حد مرکزی بتوان فرض نرمال بودن مشخصه کیفی را مناسب دانست. به هیستوگرام های زیر توجه کنید وقتی که هیستوگرام برای داده های انفرادی و وقتی برای میانگین زیر گروه ها برای همان مشخصه کیفی برای یک جامعه تولیدی رسم شده است.

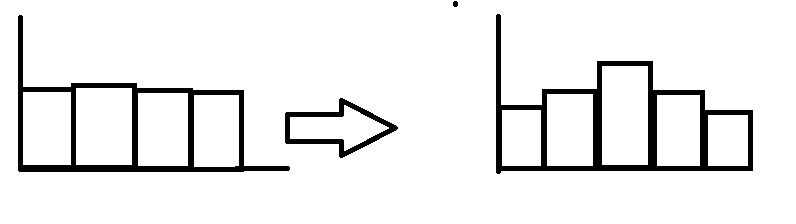
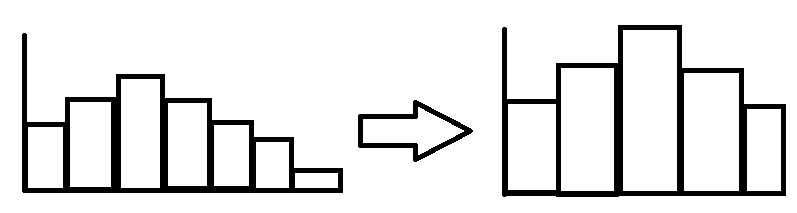
در صورتیکه از روش های فوق نیز نتیجه نگرفتیم و یا اینکه نخواهیم از نمودار استفاده کنیم میتوانیم از تبدیل هایی که در زیر معرفی میکنیم استفاده کنید.

روش های تبدیل مشخصه های کیفی غیر نرمال به نرمال

روش تبدیل معکوس

در ادامه آموزش مینی تب در این روش متغیر تبدیل شده از رابطه زیر به دست می آید.

شکل زیر مربوط به نمودار احتمال مربوط به زمان های تحویل پیتزا (xها) میباشد که توزیع آن چولگی به راست دارد اما با تبدیل متغیر y=1/x  آن گاه y ها توزیع نرمال دارند.

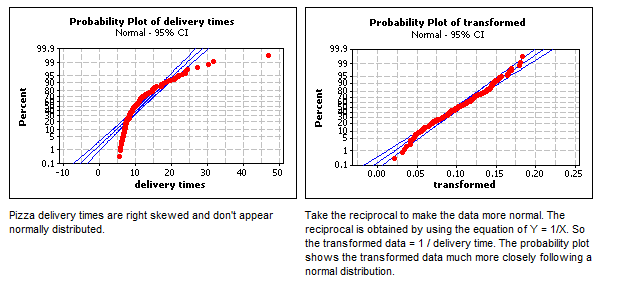
روش لگاریتمی

در این روش متغیر تبدیل شده از رابطه زیر به دست می آید:

مثال: فایل BOX-COX.MTW را باز کنید. طرح احتمال یا نمودار تقارن را برای ستون C1 مطابق مراحل زیر رسم کنید. برای رسم طرح احتمال مراحل زیر را انجام دهید.

ستون c1 را در variables وارد کنید.

OK را بزنید.

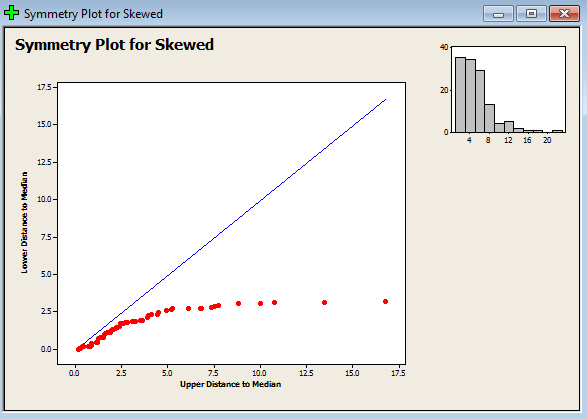
در ادامه آموزش مینی تب همانطور که میبینید مشاهدات ما توزیع نرمال ندارند و حال میخواهیم از تبدیل متغیر لگاریتمی استفاده کنیم. برای این کار مراحل زیر را دنبال کنید.

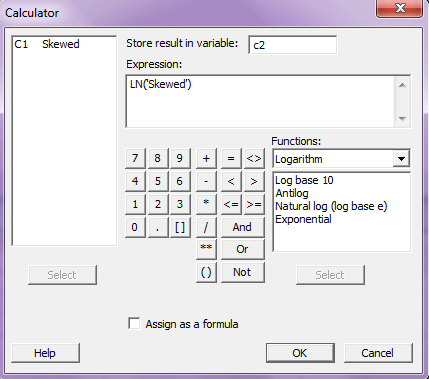
در قسمت store result in variable ستونی که میخواهید نتایج ذخیره شود وارد کنید و در قسمت Expression دستور مورد نظر را وارد کنید در این مثال با انتخاب نوع توابع  Logarithm در قسمت Natural log, Function را انتخاب کردیم و ستون c1 را در پنجره Expression در مقابل LN وارد کردیم و از ستون c2 را برای ذخیره دستور مورد نظرمان مطابق شکل زیر استفاده کردیم.

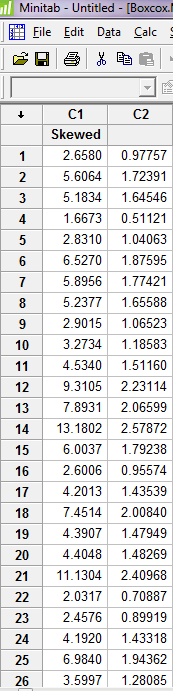
حال همان مراحلی که برای رسم طرح احتمال ستون c1 انجام دادید برای ستون  c2انجام دهید.

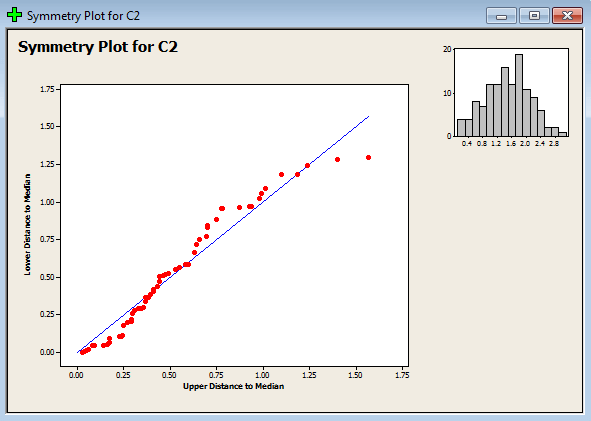
تحلیل: همانطور که مشاهده میکنید با استفاده از تبدیل متغیر داده های ستون c2 توانستند طرح احتمال نرمال را پوشش بدهند, میتوانید برای اینکه بیشتر مطمئن شوید از آزمون اندرسون دارلینگ نیز استفاده کنید.

روش ریشه دوم  (Squar Root)

مثال: فایل TILES.MTW را باز کنید. طرح احتمال یا نمودار تقارن را برای ستون C1 مطابق مراحل زیر رسم کنید.

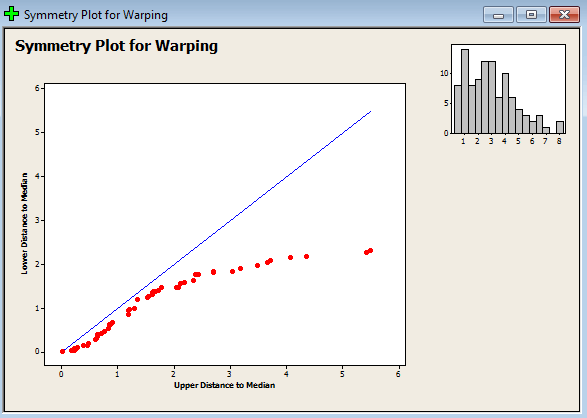
همانطور که مشاهده میکنید مشاهداتمان خط تقارن را به خوبی پوشش ندادند همچنین چولگی به راست نیز در مشاهداتمان دیده میشود حال میخواهیم از تبدیل متغیر ریشه دوم استفاده کنیم برای این کار مراحل زیر را دنبال کنید:

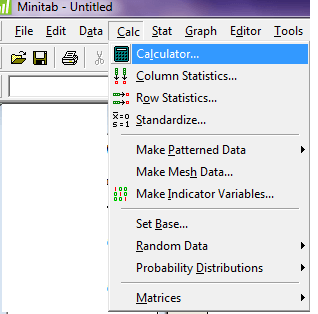
تابع Squar root  را از قسمت  Functionانتخاب کرده و ستون  c1را در مقابل آن در قسمت Expression وارد کنید و ستون  c2 را در قسمت store result in variable وارد کرده و ok را بزنید.

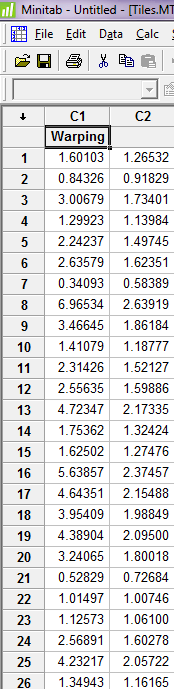
حال طرح احتمال یا نمودار تقارن را برای ستون c2 رسم کنید.

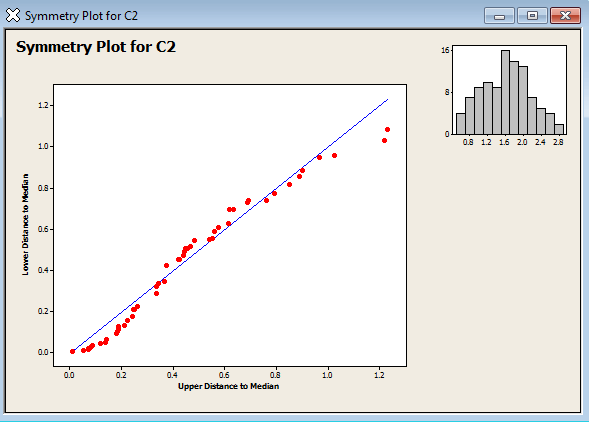
تحلیل: همانطور که مشاهده میکنید با استفاده از تبدیل متغیر داده های ستون c2 توانستند طرح احتمال نرمال را پوشش بدهند، میتوانید برای اینکه بیشتر مطمئن شوید این بار از آزمون کولموگروف- اسمیرنف نیز استفاده کنید.

روش  arcsin

تابع arcsin  در ماشین حساب نرم افزار (calculator) در قسمت توابع (Function) به نامArcsine میباشد که در صورت استفاده از این تبدیل متغیر می توانید مراحل آن را مانند مثال های قبل و برای تابع فوق تعریف کنید.

علاوه بر  ۴ روشی که گفته شد Minitab نیز ابزارهای برای تبدیل متغیر و نرمال کردن داده ها دارد که به شرح هر یک میپردازیم:

تبدیل BOX-COX

همانطور که گفته شد بعضی از داده ها از توزیع نرمال پیروی نمی کنند و میتوان با تبدیل  Box-Cox متغیرهایی را به دست آورد که توزیع نرمال داشته باشند. این تبدیل به این صورت عمل میکند که ابتدا  λ را به دست می آورد که در این روش λ طوری تخمین زده میشود که انحراف معیار متغیر تبدیل یافته حداقل شود. و داده ی جدید را از روی مقدار  λ به دست می آورد. اگر λ عددی بین -۵ تا ۵ باشد نرم افزار قابلیت تبدیل داده های غیر نرمال را به نرمال دارد.

با شرح یک مثال مطالب بالا را بهتر بیان خواهیم کرد.

مثال: فرض کنید شما برای شرکتی کار میکنید که کارش موزائیک کردن زمین است و شما نگران میزان پایداری موزائیک ها هستید. برای مطمئن شدن از کیفیت محصول شما میزان پایداری را در ۱۰ موزائیک در ۱۰ روز اندازه گیری می کنید و داده های زیر به دست می آید.

• قدم اول: فایل Tiles.MTW  را از منوی File و گزینه Open worksheet انتخاب کنید.
• قدم دوم: از منوی Graph گزینه Histogram را انتخاب کنید و روی گزینه ی With fit کلیک کنید.
• قدم سوم: در قسمت Graph variable ستون C1 را وارد کنید.
• قدم چهارم: Ok را بزنید.

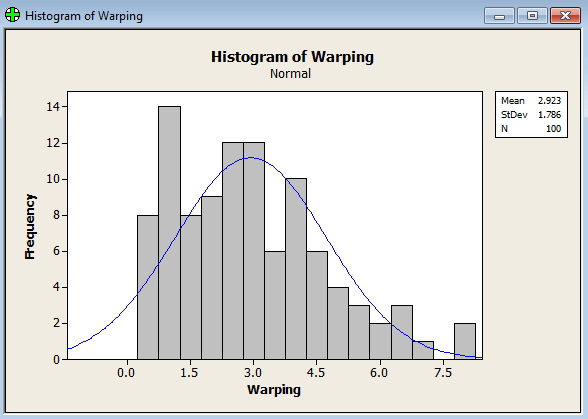
همانطور که می بینید داده های ما توزیع نرمال را به خوبی پوشش نداده است پس مسیر زیر را دنبال کنید:

قدم اول: از منوی Stat گزینه control charts را انتخاب کرده و روی box-cox transformation کلیک کنید.

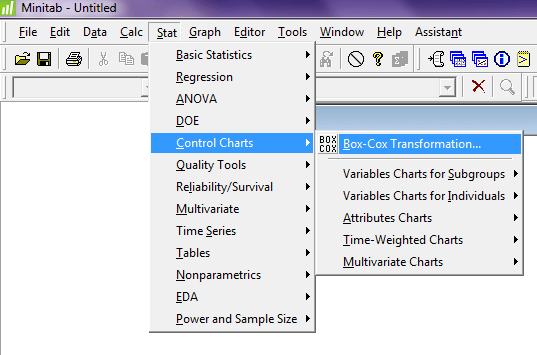
قدم دوم: چون همه ی مشاهدات را در یک ستون وارد کردیم پس در قسمت All observation for a  chart are in one column  ستون C1 را وارد کنید و چون اندازه زیر گروه برابر ۱۰ میباشد (یعنی در هر بار نمونه گیری ۱۰ نمونه گرفتیم) در قسمت  Sub Groups size عدد ۱۰ را  وارد کنید.

اگر مشاهدات هر بار نمونه گیری را سطری وارد کرده بدیم آن گاه ۱۰ سطر و ۱۰ ستون داشتیم به طوریکه هر سطر معادل هر بار نمونه گیری و هر ستون بیانگر هر مشاهده از نمونه گیری ها میباشد آنگاه به جای Observation for a subgroup are in one row of columns, All Observation for a Chart in one column را انتخاب میکردیم آن گاه در پنجره ی زیر آن ستون هایی که شامل مشاهداتمان می شود را وارد می کردیم.

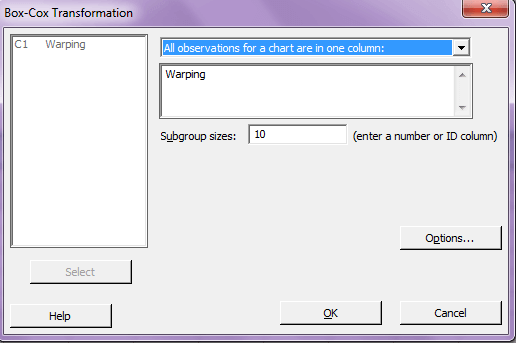
قدم سوم: به قسمت Option رفته و در قسمت Store transformed data in ستون C2 را وارد کنید تا داده های تبدیل یافته را برای شما در آن ستون وارد کند. در صورتیکه  Optimal or rounded Lambda  را انتخاب کنید نرم افزار مقدار روند شده و حتی بهینه λ را برای محاسبه متغیر تبدیل یافته استفاده میکند و اگر گزینه Other را انتخاب کنید نرم افزار از مقدار تخمین زده شده λ یا مقدار غیر روند شده استفاده میکند. هر چند اگر برای بار اول میخواهید از تبدیل متغیر  BOX-COX استفاده کنید.

ابتدا گزینه ی اول را انتخاب کنید بعد از اینکه تخمینی از λ  به دست آوردید برای بار دوم از گزینه  Other استفاده کنید.

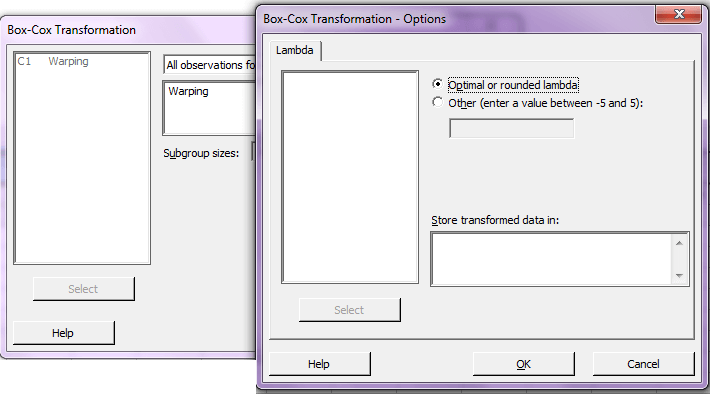
قدم چهارم: Ok را بزنید.

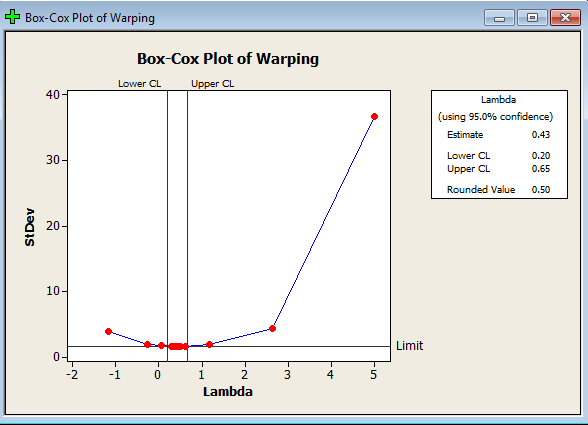
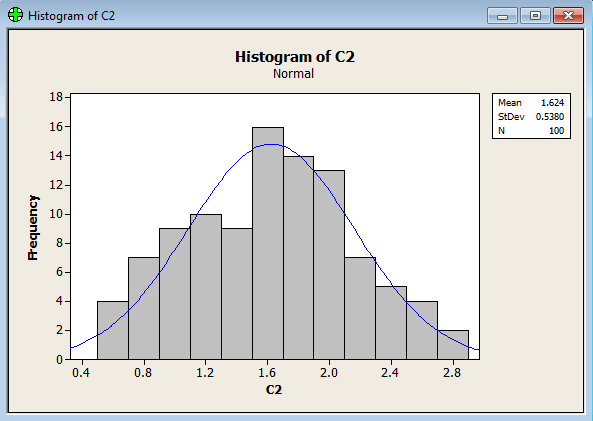
تحلیل: همانطور که مشاهده می کنید مقدار تخمینی λ=۰.۴۳و مقدار روند شده آن برابر ۰.۵ میباشد و اعداد تبدیل شده با  λ= ۰.۵ در ستون C2 وارد شده است .حال اگر Histogram ستون C2 را رسم کنید پی به نرمال شدن داده هایتان میبرید و از این به بعد هرگونه تحلیلی را روی ستون C2 برای پایداری موزائیک ها انجام می دهید.

به پایان این قسمت از آموزش رسیده ایم در مطالب بعدی به بررسی تبدیل جانسون خواهیم پرداخت.

امیدواریم از این مطلب در سایت صنایع سافت که درباره آموزش مینی تب بود، لذت برده باشید. هر سوال و نظری دارید برای ما کامنت بذارید، کمتر از یک روز پاسخ داده می‌شه 😉