آموزش Minitab برای مهندسان صنایع | (تصویری)
آموزش Minitab
آموزش Minitab نرم افزار قدرتمند در زمینه آمار و تحلیل آن به بررسی روش های تبدیل مشخصه های کیفی غیر نرمال به نرمال میپردازیم در آموزش قبلی به چند روش در این زمینه پرداخته شد برای دسترسی به مقاله های قبلی اینجا کلیک کنید. در این آموزش به موارد زیر میپردازیم :
- تبدیل جانسون (Johnson Transformation)
- فلسفه نمودارهای کنترل
- مراحل تهیه نمودار های کنترل

تبدیل جانسون (Johnson Transformation)
در ادامه آموزش Minitab روش تبدیل جانسون الگوریتم متفاوتی نسبت به روش BOX-COX دارد به طوریکه بهترین تابع تبدیل متغیر را از بین سه خانواده از توابع توزیع متغیر موجود در سیستم جانسون انتخاب میکند که این توزیع ها عبارتند از SB، SL، SU که B، L و U به ترتیب بیانگر Bounded (حددار) Longnormal و Unbounded (بدون حد) میباشد.
الگوریتم تبدیل جانسون به این صورت است که ابتدا پارامترهای مورد نیاز توابع تبدیل را تخمین میزند سپس همه ی متغیرهای غیر نرمال را با هر سه تابع تبدیل از سه خانواده ی توابع توزیع موجود در سیستم جانسون، تبدیل میکند سپس آزمون فرض اندرسون دارلینگ را برای هر سه سری متغیر تبدیل یافته انجام میدهد و هر کدام از آزمون فرض ها که بیشترین p-value را داشته باشد را به عنوان بهترین تبدیل استفاده میکند. توابع توزیع تبدیل به شرح زیر میباشند:
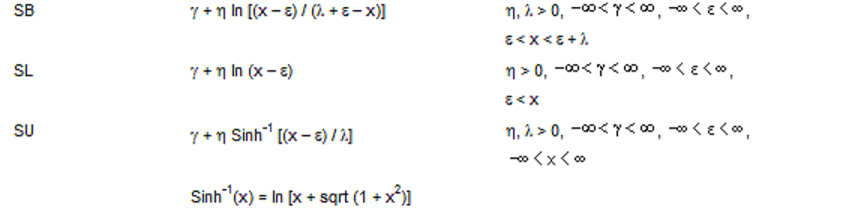
مثال: میخواهیم مشاهدات فایل Tiles.MTW در مثال قبل را این بار با تبدیل جانسون به نرمال تبدیل کنیم.
قدم اول: مسیر زیر را برای ایجاد تبدیل جانسون دنبال کنید:
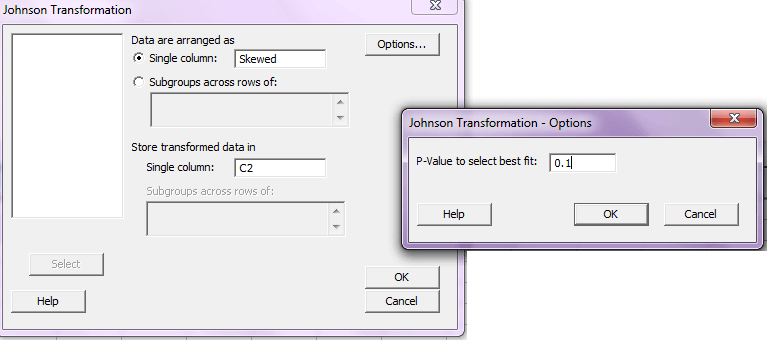
قدم دوم: در قسمت Data are arranged as اگر کلیه ی مشاهدات را در یک ستون وارد کردید، ستون مورد نظر را در مقابل single column وارد کنید، در این مثال c1 را در کادر گفته شده وارد، کنید. اگر نمونه گیری شما شامل مشاهدات مختلف میباشد و مشاهدات هر گروه منطقی را در سطرها وارد کردید.
گزینه subgroups across rows of را انتخاب کرده و ستون هایی که شامل مشاهدات شما در، هر بار نمونه گیری میباشد را انتخاب و وارد کنید.
در قسمت Store transformed data in جایی که میخواهید داده های تبدیل شده ذخیره شوند وارد کنید. باز هم اگر مشاهدات شما در یک ستون میباشد و در کادر بالاsingle column را انتخاب کردید برای ذخیره تبدیل شده مشاهداتتان فقط گزینهsingle column فعال است در غیر این صورت فقط گزینه subgroup across rows of فعال میباشد. در این مثال ستون c2 را در مقابل single column در قسمت Store transformed data in وارد کنید.
قدم سوم: options را انتخاب کنید و مقدار p-value اسمی را وارد کنید، p-value اسمی در واقع همان α خطای نوع ۱ می باشد که اگر p-value به دست آمده از α بیشتر شود فرض صفر را میپذیریم. در این مثال در کادر p-value to select best fit مقدار ۰.۱ را قرار دهید.
قدم چهارم: ok را بزنید.
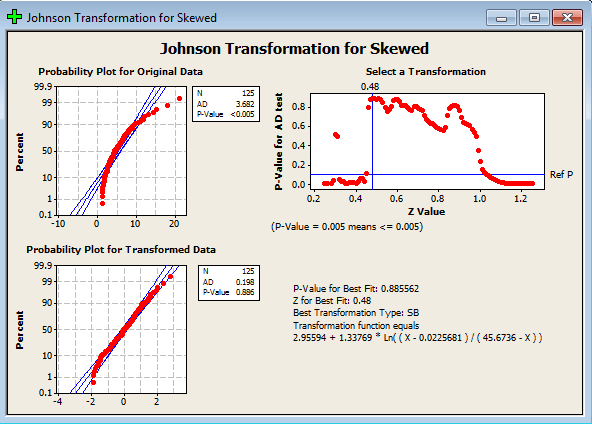
تحلیل: همانطور که از شکل پیداست Minitab طرح احتمال را هم برای قبل از تبدیل و هم برای بعد از تبدیل رسم کرده که مشاهده میکنید داده های تبدیل شده به خوبی طرح احتمال نرمال را پوشش دادند. همچنین بهترین تابع توزیع تبدیل را SB تشخیص داده که بیشترین P-value= 0.8855 را داشته است. و تابع تبدیل با تخمین های پارامترهایش نمایش داده، این تابعی است که هر y (متغیر تبدیل شده) از هر x معین (متغیر قبلی) به دست می آید و کلیه y ها در ستون c2 موجود می باشند.
تبدیل جانسون همیشه تابع مناسب را برای تبدیل کردن داده های شما پیدا نمی کند، در چنین مواقعی از تبدیل BOX-COX استفاده کنید.
در ادامه آموزش Minitab پس از اینکه کلیه ی مراحل فوق طی شد یعنی با استفاده از برگه ثبت داده ها نمونه ها جمع آوری شد، با استفاده از نمودار علت و معلول یا نمودار تمرکز نقص ها دلایل شناسایی شد و با استفاده از نمودار پارتو دلیلی از دلایل که باید بررسی شود و بهبود داده شود، انتخاب شد و پس از اینکه مشخصه کیفی قابل اندازه گیری مورد نظر تایید شد (در صورت لزوم استفاده از نمودار پراکنش) و داده ها جمع آوری شد و نرمال بودن آن تایید شد، به سراغ نمودار های کنترل می رویم که در بخش بعد به تشریح آن خواهیم پرداخت.
کلیه ی ابزارهایی که تا به حال ذکر کردیم بسته به نوع موقعیت می توانند مستقل از هم و یا وابسته به هم کار کنند و به کار گیری این نوع ابزار ها فقط بستگی به خلاقیت مهندس کیفیت دارد که کدام ابزار را در کجا و در چه زمانی به کار گیرد و نرم افزار فقط محاسبات را برای مهندس کیفیت انجام می دهد و تجزیه و تحلیل آن فقط و فقط بسته به خود مهندس کیفیت می باشد.
فلسفه نمودارهای کنترل
در ادامه آموزش Minitab پس از اینکه با ابزارهایی که در فصل گذشته آنها را شرح دادیم مشخصه کیفی مورد نظر شناسایی شد حال باید به بهبود آن بپردازیم. نمودارهای کنترل یک ابزار قدرتمند در کنترل فرآیند آماری می باشند که به وسیله ی آن مهندسان کیفیت میتوانند دلایل غیر تصادفی را از دلایل تصادفی در فرآیند تولید تشخیص داده و فرآیند را تحت کنترل دربیاورند.
هدف از ایجاد نمودار های کنترل یک آزمون فرض آماری میباشد که در آن فرض صفر برابر است با فرآیند تولید تحت کنترل میباشد و فرض یک برابر با خارج از کنترل بودن فرآیند تولید میباشد. در صورتیکه کلیه نقاط بین حدود کنترل قرار بگیرد و هیچ روند غیر تصادفی در فرآیند دیده نشود، فرض صفر را میپذیریم.
در نمودار های کنترل برای مشخصه های کیفی متغیر همواره باید دو پارامتر میانگین و انحراف معیار مشخصه کیفی مورد بازرسی، بررسی شود. هرگاه که این دو تحت کنترل درآیند فرآیند تحت کنترل است. همچنین نباید هیچگونه روند غیر تصادفی در نمودار های کنترل دیده شود.
فاز اول در نمودار های کنترل
در فاز اول در نمودار های کنترل هرگونه روند و یا علت غیر تصادفی را شناسایی کرده و آنها را برطرف می کنیم و وقتی فرآیند تحت کنترل قرار گرفت میانگین و انحراف معیار مشخصه کیفی متغیر مورد بازرسی را تخمین میزنیم.
فاز دوم در نمودار های کنترل
هدف فاز دوم تشخیص هر گونه تغییر در میانگین و انحراف معیار مشخصه کیفی میباشد که در فاز ۱ آن ها را بعد از تحت کنترل درآوردن، تخمین زده بودیم.
مراحل تهیه نمودار های کنترل
قدم اول – تعیین خطای نوع (I(α:
هدف از تعیین خطای نوع I ، تعیین حدود کنترل میباشد.
α=p{H0 صحیح باشد| رد H0 }=اعلام خطرهای اشتباهی

احتمال اینکه فرآیند خارج از کنترل قرار بگیرد و فرض صفر رد شود برابر با احتمال این است که یک نقطه از حد بالا یا از حد پایین نمودار بیرون بیفتد، پس داریم:
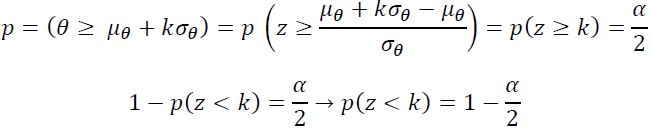
پس با استفاده از رابطه فوق با تعیین خطای نوع I میتوان ضریب انحراف معیار (K) یا حدود کنترل را به دست آورد. مثلا ۰.۲۷% = α اگر باشد داریم:
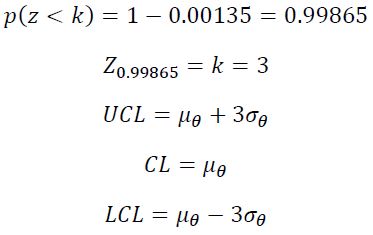
حتما بخوانید : کنترل فرایند اماری (SPC) در مینی تب
در ادامه آموزش Minitab خطای نوع I در نمودار های کنترل همان اعلام خطرهای اشتباهی میباشد مثلا اگر α برابر ( ۲۷/۱۰۰۰۰ ) باشد یعنی به طور متوسط از هر ۱۰۰۰۰ نقطه ۲۷ نقطه به صورت تصادفی از حدود کنترل بیرون می افتد که ما به اشتباه فرآیند را خارج از کنترل اعلام میکنیم در حالیکه فرآیند تحت کنترل است.
معمولاً در صنایع حساس، α را بالاتر انتخاب می کنند تا خطای نوع دوم (β) (احتمال عدم کشف تغییر) کاهش بیابد به طور مثال اگر شما یک خودروی گران قیمت داشته باشید درجه ی حساسیت دزدگیر خودرو را افزایش میدهید (α) تا اگر اتفاق خاصی افتاد سریعا پی به وجود آن ببرید (β). پس هرچه قدر مقدار α بیشتر باشد حدود کنترل تنگ تر می شود و نقاط بیشتری بیرون میفتند و ما بیشتر به دنبال دلایل آن میرویم و اگر تغییر خاصی در فرآیند باشد سریع تر آن را کشف میکنیم.
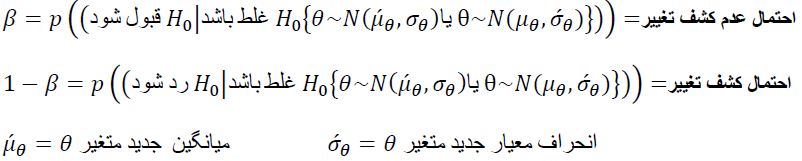
معمولاً در صنعت α را برابر ۰.۲۷% انتخاب می کنند تا حدود کنترل سه انحراف معیار بشود و اگر مشخصه کیفی حساس باشد آنگاه با تعریف قوانین حساس سازی که درباره آن بحث خواهیم کرد α را افزایش میدهیم.
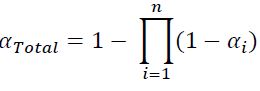
که هرچه تعداد α ها بیشتر شود αTotal افزایش می یابد. به مثال زیر توجه کنید:
فرآیند تولیدی برای یک مشخصه کیفی از محصول وقتی خارج از کنترل است که اولن نقطه ای از حدود ۳ انحراف معیار بیرون بیفتد ثانیا دو نقطه متوالیا بین حدود کنترل (۳انحراف معیار) و حدود هشدار (۲ انحراف معیار) قرار بگیرد. خطای نوع I برای نمودار کل برابر است با:
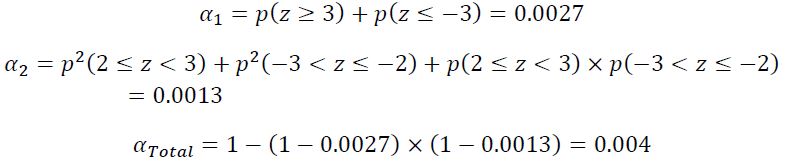
قدم دوم– انتخاب گروه های منطقی:
گروه های منطقی همان تعداد دفعات نمونه گیری می باشد. گروهای منطقی باید به گونه ای انتخاب شوند که فاصله بین هر کدام حداکثر گردد. برای مثال وقتی دو شیفت کاری در یک کارخانه وجود دارد هر شیفت یک گروه منطقی می شود و یا اگر یک بازوی پرکن برای شیشه نوشابه از t بازو تشکیل شده باشد هر بازو یک گروه منطقی می باشد. معمولاً در صنعت بین ۲۰ تا۳۰ گروه منطقی برای هر مسئله تشکیل می دهیم.
قدم سوم – انتخاب زیر گروه های منطقی:
زیر گروه های منطقی همان تعداد نمونه ها در گروه های منطقی می باشد بسته به نوع شرایط می تواند متغیر و یا ثابت باشد اما در بازرسی مشخصه های کیفی متغیر به علت بالا بودن هزینه های بازرسی و یا شاید آزمایش های تخریبی و یا بالابودن زمان آزمایش یک نمونه، زیر گروه های منطقی حداکثر ۱۲ الی ۱۵ تا می باشد.
در فاز ۱ نمودارهای کنترل معمولاً انتخاب گروههای منطقی و زیر گروههای منطقی به صورت تجربی می باشد. ایده آل ترین حالت این است که اندازه نمونه های بزرگ در فواصل زمانی کوتاه تهیه گردند. اما به خاطر مشکلاتی که در بالا ذکر کردیم معمولا ترجیح داده می شود از اندازه نمونه های کوچک در فواصل زمانی کوتاه استفاده کرد اما باز هم تاکید می کنیم شرایط است که تعیین کننده میباشد. برای مثال اگر تغییر در میانگین فرآیند تولید منجر به خسارت زیادی شود (زیاد نسبت به هزینه بازرسی) برداشتن زیرگروههای کوچک به دفعات زیاد بهتر از برداشتن زیر گروههای بزرگ به دفعات کم است. یا اگر هزینه بازرسی هر واحد نسبتاً زیاد باشد، اقتصادی ترین طرح برداشتن زیر گروههای کوچک در فواصل طولانی (مثلاً هر ۴ تا ۸ ساعت) می باشد.
در فاز ۲ در نمودارهای کنترل برای تعیین اندازه زیر گروه منطقی از شاخص های (ARL (Average Run Length و (ATS (Average Time Sampling استفاده می شود .
ARL0 =متوسط تعداد نمونه های n تایی که لازم است گرفته شود تا فرآیند را خارج از کنترل اعلام کنیم در حالیکه تحت کنترل است.
ARL1= متوسط تعداد نمونه های n تایی که لازم است گرفته شود تا پی به وجود تغییر برده شود.
ATS0 =متوسط تعداد ساعت هایی که لازم است نمونه های n تایی گرفته شود تا فرآیند را خارج از کنترل اعلام کنیم در حالیکه تحت کنترل است.
ATS1= متوسط تعداد ساعت هایی که باید نمونه های n تایی گرفته شود تا پی به وجود تغییر ببریم.
مثال: اگر در یک فرآیند تولید برای یک مشخصه کیفی با میانگین و انحراف معیار ۵ و ۱ در هر ساعت نمونه های ۴ تایی گرفته میشود. در صورتیکه میانگین فرآیند به ۶ شیفت کند الف) آن گاه به طور متوسط چند ساعت طول میکشد تا پی به وجود تغییردر میانگین فرآیند ببریم؟ ب) برای زودتر پی بردن به تغییر چه راهکاری را پیشنهاد میکنید؟ ج) هم چنین از چه اندازه نمونه ای استفاده شود تا با احتمال حداقل ۹۰% پی به وجود تغییر ببریم؟ د) کدام راه کار را پیشنهاد میکنید؟

ب) اگر به جای هر یک ساعت هر پانزده دقیقه نمونه گیری کنیم آن گاه:

ج) همانطور که میبینید هم با افزایش نمونه به ۷ تا و هم با کاهش فواصل نمونه گیری به ۱۵ دقیقه میتوان شرایط فعلی را بهبود داد و زودتر پی به وجود تغییر در میانگین مشخصه کیفی برد.
امیدواریم از این مطلب در سایت صنایع سافت که درباره آموزش Minitab بود، لذت برده باشید. هر سوال و نظری دارید برای ما کامنت بذارید، کمتر از یک روز پاسخ داده میشه 😉






